import matplotlib
if not hasattr(matplotlib.RcParams, "_get"):
matplotlib.RcParams._get = dict.get
Fit AR(p) model (Optional)#
MUDE Exam Information
The material on this page is provided to give you extra insight into time series analysis and how it is used in practice. This material is not part of the exam.
In this exercise, we will fit an AR(p) model to a time series.The time series is already stationary and we will use a method based on Likelihood Ratio Test (LRT) to choose the number of lags \(p\) to include. First we start by loading and displaying the data.
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
data = np.array([ 0.00000000e+00, 0.00000000e+00, 7.39366373e-01, 8.82012627e-01,
-2.17941679e-01, 1.54974089e+00, -8.98443756e-02, 1.00141169e+00,
2.42524470e-01, -1.02361298e-01, -1.10553118e+00, 3.04987823e-01,
-8.69761112e-01, -1.11315875e+00, -4.24734667e-01, 1.45309595e-01,
5.42097653e-01, 3.77506030e-01, -7.33921297e-01, -2.31148958e-01,
-1.76689101e+00, -6.79235565e-01, -4.00350747e-01, -2.35241349e-01,
-9.07637426e-01, 2.13326549e-01, 2.18065416e-01, -1.60757882e+00,
-2.07263765e+00, -1.18111332e+00, -1.47885555e+00, -1.89930627e+00,
-1.57038634e+00, -2.07430124e+00, -1.03020905e+00, -1.05763683e+00,
-7.48698592e-01, -1.57544551e+00, -2.50491924e+00, -1.42908722e+00,
-1.08312118e+00, -1.80363252e+00, -1.04630764e+00, -1.71038000e+00,
-1.71349481e+00, -1.44771288e+00, 4.20877715e-01, 5.07187528e-01,
-4.87173992e-01, 3.24049379e-01, 2.59529792e-01, 5.04614412e-01,
4.73901121e-01, 2.72281199e-01, -1.41652577e+00, -1.39176422e+00,
-8.29335646e-01, -4.20523393e-01, -8.41985423e-02, 9.41730115e-02,
-1.50729414e+00, -8.74161867e-01, 2.01810837e-01, -2.17818122e+00,
-5.92488929e-01, 1.07042695e+00, 4.37509451e-01, 7.22526958e-01,
1.22407607e+00, 7.70631751e-01, 1.50808058e+00, -8.50142466e-01,
-3.73831479e-01, 1.35391870e+00, 2.18917967e+00, 2.57638726e+00,
2.70701733e+00, 1.36794873e+00, 1.29999210e+00, 1.91501107e+00,
1.59349872e+00, 1.97732807e+00, 2.49992433e+00, 1.93175636e+00,
1.47660557e+00, 1.17536071e+00, 1.39557491e+00, 1.44857054e+00,
7.89092903e-01, -6.46392931e-01, 2.95521216e-01, -1.08968239e-01,
-3.85438702e-01, -3.58086137e-01, -5.09981434e-01, -2.05496939e+00,
-3.64585529e-01, -3.96458235e-02, 3.53929808e-01, 1.58901411e+00,
9.53132950e-02, 7.67470550e-01, 1.15384857e+00, 7.96439922e-01,
9.76627268e-01, 3.47042888e-01, 1.00590245e+00, 1.50082738e-01,
2.37379710e-01, 1.96873095e+00, 2.20072042e+00, 1.56046852e+00,
6.64436129e-01, 2.96544445e-01, 1.72227831e+00, 1.10644286e+00,
1.63238235e+00, 6.63026552e-01, 3.61978366e-01, 6.45668467e-01,
1.27851822e+00, 2.65148989e+00, 9.99420989e-01, 3.58085372e-01,
-4.62291606e-01, 9.37518000e-01, 1.23164122e+00, -3.12475856e-01,
1.36065286e-01, -6.16493968e-02, 6.69941343e-01, -3.42736465e-01,
-1.34703063e+00, -1.67947236e+00, 5.69358500e-01, 5.83468985e-01,
7.41796103e-01, 6.39326772e-01, 2.10445565e-01, 3.92168977e-01,
6.40725851e-01, 8.99547148e-01, 1.00500576e+00, -8.71818439e-02,
4.04000299e-02, 8.70113665e-01, -1.44264848e-01, 5.39213359e-01,
6.66901278e-01, 8.72123995e-01, 1.84825136e+00, 1.10125095e+00,
9.95721987e-01, 6.26088972e-01, 7.62512607e-01, 1.16511511e-01,
4.22571492e-01, 9.89100398e-02, 5.49712966e-01, -1.56725388e-01,
4.27536063e-01, 2.05360843e-01, -5.64858058e-01, -2.69873034e-02,
-9.37568737e-01, 8.65612664e-01, -3.69365069e-01, 2.39337297e+00,
8.60106273e-01, 3.29178916e+00, 1.71736403e+00, 2.13874664e+00,
1.48955823e+00, 1.48006688e+00, -6.88803421e-01, -3.24234835e-01,
-1.24331549e+00, -6.66509456e-01, -9.04246649e-01, -1.90451608e+00,
-9.87961104e-01, -5.48066393e-01, -1.57398280e-01, -4.07591149e-01,
1.15083345e+00, 5.88506643e-01, -5.92900945e-01, -3.44438570e-01,
-7.29310067e-01, 5.74169750e-01, 4.04520673e-01, -2.20288636e-01,
-2.77120327e-02, 9.88213495e-02, -1.09190567e+00, 7.19825871e-02,
-9.84122442e-01, -1.80535953e-01, -5.14311755e-01, -6.47274166e-01,
-7.56479222e-01, 1.08118071e-01, -9.57690388e-01, -1.57851451e+00,
-1.31524418e+00, -1.40305337e+00, -2.54378176e+00, -1.84970651e+00,
-2.32341947e+00, -1.60528868e+00, -6.02478175e-01, -1.51805873e+00,
-6.37833606e-01, 2.76604125e-01, -2.33841731e-01, -1.36818872e+00,
-5.72040718e-01, 6.55878864e-01, 1.13125989e+00, 2.20828257e+00,
1.08565693e+00, 1.28351412e-01, 5.46169855e-01, 5.93641545e-01,
6.04036418e-01, 3.49137797e-01, -1.83183726e-01, 6.16385128e-01,
2.10314828e-01, 3.45091013e-01, -6.13021032e-01, 1.26537948e+00,
7.35755004e-01, -1.91878585e-01, -1.02143047e+00, -8.41844559e-01,
-9.04793546e-01, 9.84542133e-01, 4.52293503e-01, -8.17515258e-01,
-2.38201270e-01, 2.09588612e-01, 3.10936455e-01, -6.13386042e-02,
4.45269097e-01, -1.22797128e+00, -2.25841101e-01, 6.68332290e-01,
2.14404817e+00, 6.70914150e-01, 1.79696828e+00, 2.49805512e+00,
3.64554459e-01, -2.28644444e-01, -1.09699150e+00, -1.03731317e+00,
-3.96379156e-01, -1.38065556e+00, -3.82528623e-01, -1.02683833e+00,
-1.51626243e+00, -3.08281555e-02, -1.61811653e-01, -3.08337884e-01,
6.78369204e-02, -1.07006199e+00, -5.79365880e-01, 2.51602954e-01,
-1.39343464e+00, -1.05284048e+00, -1.06705460e+00, -4.86584542e-01,
-2.45306112e+00, -1.49506393e+00, -2.64593592e+00, -3.01740934e+00,
-1.77716519e+00, -2.71373930e+00, -2.03803161e+00, -1.20648230e+00,
-1.03999481e+00, -9.91418930e-01, -9.91249144e-01, -8.44261622e-01,
-1.50101351e+00, -1.25887947e-01, -1.40571889e+00, 4.88496184e-01,
-8.47740317e-01, 2.53055261e-01, 4.07728654e-01, 3.71441178e-01,
2.60954268e-01, 6.91881170e-01, 1.35204560e+00, 1.66126779e+00,
3.87633110e-02, 5.74308554e-02, -4.90039426e-01, -3.51960048e-01,
-3.40826500e-01, -4.29096877e-01, -1.51329551e-01, 7.01787314e-01,
-6.57970553e-01, 6.63866169e-01, 3.83965676e-01, 9.80863226e-01,
1.26264195e+00, 1.60111452e+00, 1.71967437e+00, 1.27973984e+00,
-1.32558645e-01, 1.04491727e+00, 1.02027173e+00, 1.30056175e+00,
1.24801760e+00, 1.83402451e+00, 1.53001108e+00, 1.71737846e+00,
1.57527834e+00, 2.04640540e+00, 2.42281956e+00, 8.27044471e-01,
2.10345979e+00, 1.06201511e+00, 1.47960807e+00, 9.71628403e-01,
5.21057069e-01, 5.03029167e-01, 4.21029664e-01, 1.10529512e+00,
6.54941435e-01, -4.79959006e-01, 8.01560793e-01, 3.78517418e-01,
5.08672026e-01, 1.68601802e-01, -3.90663606e-02, 1.62149508e+00,
1.45669361e+00, 1.24135471e+00, -7.00934966e-01, -9.13895360e-01,
4.83077266e-01, 4.50055520e-01, -1.17878557e+00, -6.26810617e-01,
7.11486395e-02, -1.66610081e-01, -4.00110856e-01, -1.59543090e-01,
3.69607167e-01, 1.05543185e+00, 1.27906214e+00, 1.23240685e+00,
2.09226813e+00, 8.90031863e-01, 2.22894835e+00, 6.97854347e-01,
1.09524514e+00, 3.24695184e-01, 7.28042788e-04, -4.45720862e-01,
-5.73334022e-02, 1.23575766e+00, 1.31635328e-01, 8.67518743e-01,
1.56059963e+00, 6.31070006e-01, 1.04464919e+00, -8.84947785e-01,
1.31704400e+00, 9.86125573e-01, 2.02759151e+00, 1.48625969e+00,
3.72770752e-02, 1.67338281e+00, 1.82601616e+00, 4.32808593e-01,
1.91126665e+00, -1.40124317e-02, -6.15394675e-01, 1.24704749e+00,
1.30533712e+00, 1.15308051e+00, 1.59741846e+00, 1.07918179e+00,
3.55408514e-01, 1.15370940e-01, -8.76059920e-01, -1.33802778e+00,
1.85639559e-01, -2.42649844e-01, -1.02996400e+00, 4.39484660e-01,
-1.07934516e+00, -2.43198782e-01, 7.12058866e-01, -3.74227516e-01,
8.88699033e-01, -3.97313023e-01, 2.86881825e-01, 4.79528683e-01,
1.96059535e+00, 1.90794329e+00, 1.21424753e+00, -9.31731368e-03,
-3.57476964e-01, -6.54898612e-01, -8.55912921e-01, 4.82253263e-01,
7.82414953e-02, -1.16817948e-02, 1.02454754e-01, 4.75701199e-01,
2.87974276e-02, 7.23507213e-01, 1.11294268e+00, 1.54304889e+00,
2.55006078e+00, 1.97330796e+00, 4.55008481e-01, 9.08155981e-01,
-3.16408466e-01, -9.11070592e-01, -1.19885254e+00, -1.49425998e+00,
-3.70184461e-01, -1.33816807e+00, 9.85350424e-02, -4.17349272e-01,
9.88553840e-01, 3.70111247e-01, 9.00847240e-01, 1.63814995e-01,
1.36672484e+00, 1.06231592e+00, 6.86277219e-01, -1.36714690e-01,
-2.10193654e-01, 1.03258012e+00, 8.99548082e-01, 9.98615963e-01,
-6.21537335e-01, 5.45974283e-01, 7.76469620e-01, 1.50429680e+00,
7.48151842e-01, 4.43051388e-01, 8.08282554e-01, 4.68694570e-01,
-9.76716836e-01, -5.65906274e-01, -9.79593683e-01, 9.32812962e-01,
1.09446918e+00, 1.53156737e+00, 6.07745371e-01, 8.90444322e-01,
2.58227806e-01, 1.08671023e+00, 1.96989982e-01, -6.81961888e-01,
-9.03880880e-01, -9.70885459e-01, -2.65810797e-01, -4.29907694e-01,
4.06336577e-01, 4.78504065e-01, 1.27168476e-01, 1.46771856e+00,
1.36753502e+00, 4.02762296e-01, 3.64682830e-01, -3.78703131e-01,
2.96891803e-01, -7.54382156e-01, 1.28006210e+00, -6.86188078e-02,
1.20052445e+00, -1.66199770e-02, 6.87313607e-01, 7.05341388e-01,
1.09361043e+00, -5.62887584e-02, -1.02212099e-01, -3.98220516e-01,
-6.35448516e-01, -1.23454870e+00, 3.30223301e-01, 6.36362445e-01,
5.95033506e-01, -1.21809241e-01, -1.01669089e+00, -2.83311223e+00,
7.05074907e-02, -8.14821554e-01, -1.09891995e-01, 8.46936249e-02,
9.89420750e-01, 1.19584073e-01, -2.55632428e-01, 1.78726604e+00,
1.15139811e+00, 7.30881522e-01, 3.73337741e-01, -8.84734893e-01,
9.15512809e-01, 3.48834785e-01, -6.83496242e-01, 1.44386150e+00,
9.40535741e-01, 1.61809060e+00, 5.90633602e-01, -1.81711114e-01,
-5.43810530e-01, -9.47633330e-01, -1.08840745e+00, -2.12147676e+00,
-1.93298030e+00, -1.81721802e+00, -8.60719118e-01, -5.87439117e-01,
-4.42704828e-01, -7.71683303e-01, -7.09202014e-01, -1.01576221e+00,
-1.00405087e+00, -2.35322370e+00, -1.55945639e+00, -1.93038555e+00,
-1.77439000e+00, -7.31110363e-01, -1.11229932e+00, -5.53420963e-01,
-2.54646158e+00, 1.30171409e-01, 9.58477732e-02, -1.67702799e-01,
1.07557175e-01, 9.39260555e-01, -1.01729680e+00, -7.51412913e-03,
2.50457369e-02, -7.93504732e-01, 7.66769888e-02, -4.91396297e-01,
-6.23168011e-01, 5.56471001e-01, -1.47489436e+00, -1.80051893e-01,
-9.29699644e-01, -2.86270863e-01, -4.03645146e-01, -1.59207517e+00,
-1.51789958e+00, -5.17777627e-01, -1.44915841e+00, -2.82704891e-01,
-7.77895523e-01, 4.24394846e-02, 6.39871136e-01, -8.25068603e-01,
1.70283470e-01, -3.04672894e-01, 7.57377629e-01, 2.81579728e-01,
9.00245371e-01, 4.38308567e-01, 6.62981478e-01, 2.26340506e-01,
6.55124877e-01, -4.74574465e-02, 5.83536959e-01, 3.30224150e-01,
1.74725260e+00, 2.92914951e-01, 6.53733549e-01, 1.90472489e+00,
2.13062770e+00, 8.29887814e-01, 1.78665718e+00, 3.36002901e+00,
1.80680569e+00, 7.24783016e-01, -8.31104542e-02, 1.06971812e+00,
-7.92409025e-01, -1.12136978e-02, 1.36246834e-01, -3.96155791e-01,
-5.17756929e-02, -5.53090799e-01, 1.27895232e-01, -1.14333497e-01,
5.69661453e-02, -1.30418263e+00, -4.20354967e-01, -9.69997976e-02,
1.25838428e+00, 7.67147245e-01, -1.96356797e-01, -7.25875722e-01,
9.13773378e-03, -1.92841740e-01, 1.36680690e+00, 7.85367122e-02,
1.43978042e+00, 3.53036371e-01, 3.21726380e-01, 7.27328771e-01,
3.42772844e-01, -8.08014869e-01, -7.84040601e-01, -9.71464217e-01,
-3.38824750e-01, -1.28809967e+00, -3.87057040e-01, -9.72010741e-01,
-1.39459163e+00, -5.41007591e-01, -1.38221603e+00, -1.88021763e+00,
-1.25018544e+00, -8.95854470e-01, -2.42330929e+00, -1.93677650e+00,
-2.85864261e+00, -2.28733387e+00, -3.12822402e+00, -2.65251704e+00,
-3.18254573e+00, -2.43695779e+00, -3.33016093e+00, -2.56150214e+00,
-2.40580874e+00, -2.04801271e+00, -9.45886359e-01, -4.80283888e-01,
-9.02308417e-01, 4.39017348e-02, 1.40193351e+00, 1.12539513e-04,
1.20803285e+00, -1.05656599e-01, -8.15697707e-01, -1.33205596e+00,
-1.11363610e+00, -1.55571463e+00, -2.35843487e+00, -3.80555093e-01,
-1.42667129e-01, 1.87343826e-01, -9.03622737e-01, 1.58042120e+00,
9.14429754e-01, 1.43619930e+00, 1.91061472e+00, 9.74028580e-01,
5.34409977e-01, -1.90812107e-01, 1.31103428e+00, 2.35584323e+00,
1.02766574e+00, 4.17273584e-01, 1.34848289e+00, 1.26365466e+00,
1.24666532e-02, 2.31648529e-02, -2.83896716e-01, 3.74971332e-01,
1.59599098e-01, 6.12558213e-01, -8.27835045e-02, 7.12749888e-01,
1.34679669e+00, 1.12912214e+00, 5.15484989e-01, 6.28624387e-01,
-2.45869042e-01, 3.27209328e-01, -4.96825605e-01, 1.31898972e-01,
-1.81544836e-01, 5.41585156e-01, 8.66005696e-01, -1.34887158e+00,
-1.05298192e+00, -3.55200747e-02, -6.17742426e-02, 3.15934090e-01,
7.58516075e-01, -1.28638664e-01, -3.62368353e-01, 1.85925648e-01,
1.10367660e+00, -4.71440744e-02, 1.15255335e+00, 9.62837157e-01,
1.01530785e+00, 5.16531675e-01, 5.18742934e-01, 7.35507772e-01,
3.67891288e-01, -9.15120567e-01, -7.12922515e-01, 7.95935851e-01,
-8.24176529e-01, 1.01923996e-01, -7.19323604e-01, -8.11150057e-01,
2.11116100e-01, 7.08622195e-01, 1.20049183e+00, 1.07098285e+00,
3.68214610e-01, 3.54257026e-01, 7.05818294e-02, -3.39895972e-01,
-1.16645409e-01, 1.82229015e-01, -7.70677164e-01, -9.31566188e-01,
1.47087451e-01, 1.06149338e+00, 1.15550485e+00, 8.00273717e-01,
1.55176802e+00, 2.10226314e+00, 3.95218245e-01, 2.77919345e-01,
1.46034669e+00, 1.19407058e+00, 1.95311543e+00, 1.77257448e+00,
4.11952827e-01, -1.03775982e-01, 1.60578453e-01, -5.78448463e-01,
-6.74402250e-02, -5.38429388e-02, -9.56971433e-01, -1.77622550e-01,
-2.58961602e-01, 6.06878724e-01, -2.61909649e-01, -3.05580909e-01,
-6.47796264e-01, -1.38091098e+00, -8.81668249e-01, -4.40749857e-01,
-9.64560692e-01, -9.02942803e-01, -1.51032638e+00, -9.78485228e-01,
-1.35448247e+00, -5.20396184e-01, -1.63593472e-01, 1.39960962e-01,
7.61197724e-01, -1.80842551e-01, -6.66113910e-01, -2.03078431e-02,
4.59656603e-02, -6.24886605e-01, -7.55849348e-01, -2.62076342e-01,
1.10954752e-01, -9.38955437e-01, -3.39143906e-01, -8.10682908e-01,
4.23887208e-01, 8.61515571e-01, 6.65772041e-01, 2.31012501e+00,
2.24641806e+00, 2.03232659e+00, 2.50357257e+00, 2.28339898e+00,
1.95069044e+00, 1.63523854e+00, 1.37286544e+00, 2.43219243e+00,
2.55092337e+00, 1.76595226e+00, -8.62412017e-02, 1.59579762e+00,
5.08483834e-01, 4.15151476e-01, 6.93189435e-01, 9.21821403e-01,
1.29025111e+00, 7.93774884e-02, 6.80210192e-02, -6.94808049e-01,
-3.51609274e-01, 1.47062707e+00, 5.89348866e-01, 2.11627876e+00,
6.52185541e-01, 1.26132338e+00, 6.98691324e-01, 3.48855150e-01,
-1.33109062e+00, -1.47342324e+00, 1.09013417e+00, -1.11974953e-02,
4.17028815e-01, 3.76022584e-01, 2.70449474e-01, 5.42963217e-01,
-2.79830499e-01, -4.99062723e-01, 1.69929223e-01, -6.13573591e-01,
-7.45367870e-01, -9.69028857e-01, -2.33629353e+00, -2.03188486e+00,
-1.81089730e+00, -1.49790534e+00, -1.99281756e+00, -1.81819238e+00,
-1.47388646e+00, -1.81642763e+00, -2.32034092e+00, -9.46747332e-01,
-6.22658430e-01, -6.70254068e-01, -1.25268470e+00, -5.51126224e-01,
1.12351647e+00, 7.41654766e-01, -4.56727439e-01, -5.36036952e-01,
3.79299501e-01, 6.10543198e-01, 1.04647975e+00, -5.26770962e-02,
9.10931820e-01, 2.88667270e-01, 1.43372970e+00, 8.83455823e-01,
7.40768747e-01, 1.02984778e+00, -1.46106980e-01, 3.70249466e-01,
-5.48979579e-01, -1.64568153e+00, 3.48798867e-01, 2.17017707e-01,
-1.37474632e-01, 9.53455170e-01, -7.06646698e-01, -7.85727930e-01,
3.17707117e-01, -7.46688323e-01, 5.72143464e-01, 1.22252222e+00,
6.49886478e-01, 1.11199626e+00, 2.98352821e+00, 2.47769388e+00,
1.18576263e+00, 5.33805666e-01, 2.10096587e+00, 1.59574729e+00,
1.31832487e+00, 3.84267233e-01, 1.18968620e+00, 2.39827315e+00,
1.53984467e+00, 1.73049810e+00, 3.03364076e-01, -7.57727641e-01,
-6.75717011e-01, -1.05885226e+00, -7.91154756e-01, 2.93195048e-01,
-8.55754313e-01, -2.03581616e-01, -4.70712707e-01, 4.37962580e-01,
8.03218956e-01, 5.72756250e-01, -2.09349498e-01, 6.93622013e-01,
1.52325261e+00, 7.46335450e-01, 1.04179128e+00, 6.93180243e-01,
6.15903795e-01, 1.72977174e+00, -8.97999867e-02, 2.50893420e+00,
1.78139472e+00, 1.30976033e+00, 5.56591118e-01, 2.35011371e-01,
-3.85188166e-01, -4.47569045e-01, -1.24490106e-02, -3.24913641e-02,
7.26347917e-01, -7.93962450e-01, -1.13628472e+00, -3.70710503e-01,
-1.41297811e+00, -7.05695681e-01, -6.89106682e-01, -8.76022961e-01,
-6.35076122e-01, -2.20968410e+00, -1.66157685e+00, -2.78915712e-01,
-7.35596283e-01, -7.08503954e-01, 1.98219493e-01, -1.47695316e+00,
-4.35808912e-01, -1.13217275e-01, -1.08390134e+00, 8.56553143e-01,
5.19019577e-01, 4.48514228e-01, -1.49052322e-01, 1.64228141e-01,
-2.38744808e-02, -9.94880817e-01, -1.09619291e+00, -1.23149681e+00,
-2.29443615e+00, -9.24490557e-01, -1.41361200e+00, -1.14823308e+00,
6.35477621e-01, 5.99331444e-01, -5.51869204e-01, 4.57836691e-01,
1.36644386e+00, 1.99158100e+00, 1.05917265e+00, -6.20214682e-01,
-3.03986356e-01, 9.21210441e-01, 1.86984440e+00, 7.19809989e-01,
2.24614850e-01, 1.83986293e+00, -4.98484113e-01, 8.48969414e-01,
1.46145990e+00, 4.64898199e-01, 5.95667867e-01, -1.65015303e-01,
4.98926356e-01, 1.27696976e+00, 6.31788684e-01, 9.02383220e-01,
9.09245114e-02, -8.33510548e-01, -7.73376882e-01, 4.20514784e-01,
4.00816394e-01, 4.23429604e-01, 7.03190294e-01, 2.45607983e-01,
1.12766363e-01, 2.29990495e-01, 1.44303637e-01, 2.98763762e-01,
1.66542808e+00, 2.09103268e+00, 1.90449043e+00, 1.72099303e+00,
1.25933300e+00, 2.29352112e+00, 1.97652899e-01, 1.17981554e+00,
-1.11019238e+00, -3.31291763e-01, -4.81943208e-01, -1.57380538e+00,
-8.01543386e-01, -1.57373293e+00, -6.11527712e-01, -1.17852491e+00,
4.34070610e-01, -9.47518014e-01, -1.21053098e+00, -8.52856246e-01,
-1.25192446e+00, -1.30987448e-01, 2.71523161e-01, -1.02593613e+00,
4.19178470e-01, -3.32333953e-01, -7.02741725e-01, 1.18590220e+00])
#plot data
plt.figure(figsize=(12, 4))
plt.plot(data)
plt.xlabel('Time')
plt.ylabel('Y(t)')
plt.title('Generated stationary Time Series')
plt.grid(True)
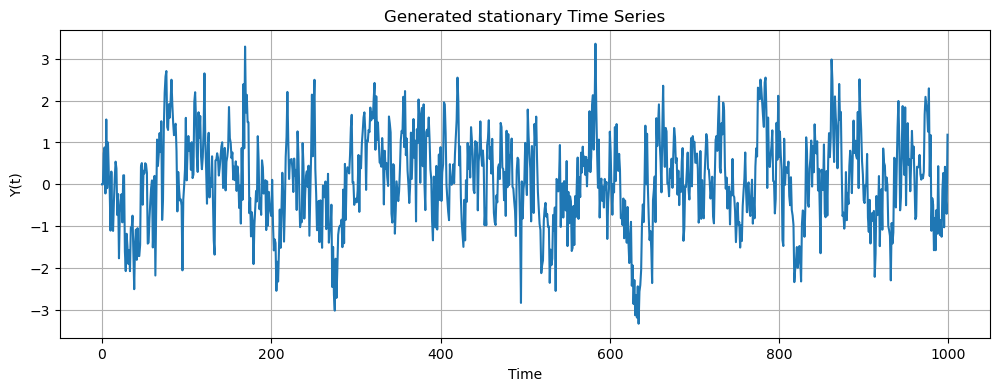
Next we can use plot_acf to plot the autocorrelation function of the time series. From the resulting plot we can see that that there is autocorrelation present in the data.
# Plot the ACF of the time series
fig, ax = plt.subplots(figsize=(12, 4))
plot_acf(data, lags=40, ax=ax)
ax.grid(True);
ax.set_xlabel("Lag")
ax.set_ylabel("ACF")
Text(0, 0.5, 'ACF')
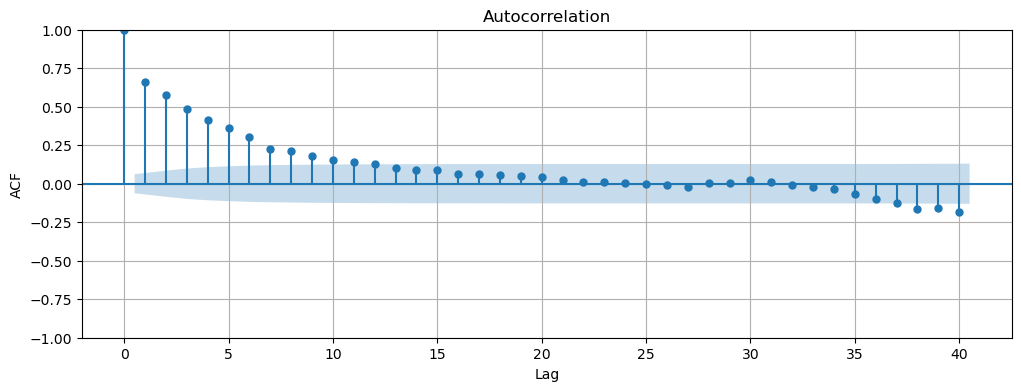
To make sure that we have selected the correct number of lags, we can test for significance using the likelihood ratio test (LRT). LRT is similar to the GLRT from Observation theory, but now we have made some assumptions on the standard deviations of the observations. We will apply the LRT to the AR(1) vs AR(2) and AR(2) vs AR(3) models.
The AR(1), AR(2) and AR(3) models are defined as follows:
AR(1): \(S_t = \phi_1 S_{t-1} + \epsilon(t)\)
AR(2): \(S_t = \phi_1 S_{t-1} + \phi_2 S_{t-2} + \epsilon(t)\)
AR(3): \(S_t = \phi_1 S_{t-1} + \phi_2 S_{t-2} + \phi_3 S_{t-3} + \epsilon(t)\)
Since we need \(S_{t-3}\) we will have \(y = S[3:]\)
from scipy.stats import chi2
y = data[3:]
s1 = data[2:-1]
s2 = data[1:-2]
s3 = data[:-3]
n = len(y)
# AR(1) model
X1 = np.column_stack((s1)).T
phi_ar1 = np.linalg.inv(X1.T @ X1) @ (X1.T @ y)
e1 = y - X1 @ phi_ar1
rss1 = e1.T @ e1
# AR(2) model
X2 = np.column_stack((s1, s2))
phi_ar2 = np.linalg.inv(X2.T @ X2) @ X2.T @ y
e2 = y - X2 @ phi_ar2
rss2 = e2.T @ e2
# AR(3) model
X3 = np.column_stack((s1, s2, s3))
phi_ar3 = np.linalg.inv(X3.T @ X3) @ X3.T @ y
e3 = y - X3 @ phi_ar3
rss3 = e3.T @ e3
# test ar(1) vs ar(2) using log likelihood ratio test
dof = 1
crit = chi2.ppf(0.95, dof)
test_stat = n * np.log(rss1 / rss2)
print('AR(1) vs AR(2) test statistic:', test_stat, 'Critical value:', crit)
if test_stat > crit:
print('Reject AR(1) in favor of AR(2)')
else:
print('Fail to reject AR(1)')
# test ar(2) vs ar(3) using log likelihood ratio test
dof = 1
crit = chi2.ppf(0.95, dof)
test_stat = n * np.log(rss2 / rss3)
print('AR(2) vs AR(3) test statistic:', test_stat, 'Critical value:', crit)
if test_stat > crit:
print('Reject AR(2) in favor of AR(3)')
else:
print('Fail to reject AR(2)')
AR(1) vs AR(2) test statistic: 65.33452260973341 Critical value: 3.841458820694124
Reject AR(1) in favor of AR(2)
AR(2) vs AR(3) test statistic: 3.5153713615375244 Critical value: 3.841458820694124
Fail to reject AR(2)
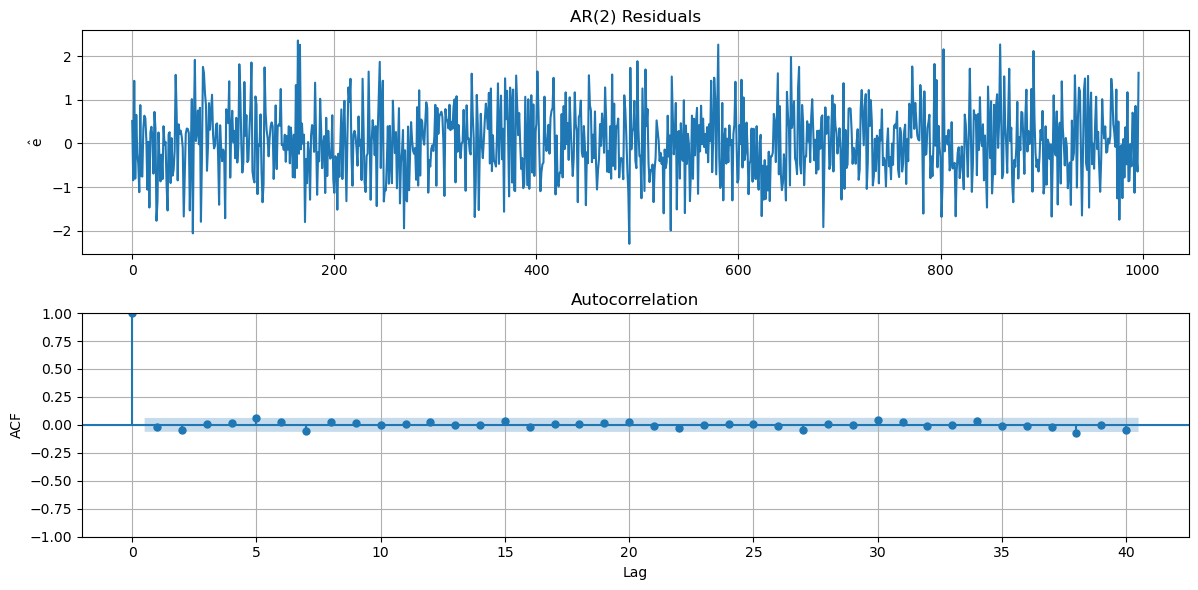
From the LRT results we can see that an AR(2) model is the best fit for the data. Finally we will fit the AR(2) model to the data and plot the residuals. The residuals should be white noise, which is confirmed by the ACF plots of the residuals.
# plot the residuals
fig, ax = plt.subplots(2,1,figsize=(12, 6))
ax[0].plot(e2)
ax[0].set_title('AR(2) Residuals')
ax[0].grid(True)
ax[0].set_ylabel('$\mathrm{\hat{e}}$')
plot_acf(e2, lags=40, ax=ax[1])
ax[1].set_xlabel("Lag")
ax[1].set_ylabel("ACF")
ax[1].grid(True)
fig.tight_layout()
sigma_e2 = np.std(e2)
var_phi2 = sigma_e2**2 * np.linalg.inv(X2.T @ X2)
sigma_phi2 = np.sqrt(np.diag(var_phi2))
# print the AR(2) coefficients with confidence intervals
print('AR(2) Coefficients:')
print('Phi_1 = ', round(phi_ar2[0], 4), '+/-', round(1.96 * sigma_phi2[0], 4))
print('Phi_2 = ', round(phi_ar2[1], 4), '+/-', round(1.96 * sigma_phi2[1], 4))
AR(2) Coefficients:
Phi_1 = 0.4961 +/- 0.0601
Phi_2 = 0.2523 +/- 0.0602
Attribution
This chapter was written by Alireza Amiri-Simkooei, Christiaan Tiberius and Sandra Verhagen. Find out more here.
