Exercise 2: Cargo airplane (Optional)

MUDE Exam Information

For the exam, you are expected to have a clear understanding behind the Simplex method and how to do it. you will not need to do the calculations by hand in the exam or on Friday’s assignment.

Original problem

A cargo airplane has three compartments for storing freight: Front, central and rear. Each one of those compartments has the following limitations in weight and space:

Compartment	Weight (\(\text{ton}\))	Volume (\(\text{m}^3\))
Front	8	12000
Central	12	10000
Rear	14	6000

There are four cargo types, and the following maximum cargo (of each type) is available to be transported from a warehouse:

Cargo	Maximum cargo available (\(\text{ton}\))	Unit Volume (\(\cfrac{\text{m}^3}{\text{ton}}\))	Unit profit (\(\cfrac{\text{€}}{\text{ton}}\))
Type I	18	180	590
Type II	14	250	580
Type III	20	300	580
Type IV	12	80	600

Task 1

Build the mathematical programming model in order to define the amount of cargo of each type that should be transported and how it should be distributed in order to be efficient during the flight

Solution

Decision variables

	Front	Center	Rear
Type I	\(x_{11}\)	\(x_{12}\)	\(x_{13}\)
Type II	\(x_{21}\)	\(x_{22}\)	\(x_{23}\)
Type III	\(x_{31}\)	\(x_{32}\)	\(x_{33}\)
Type IV	\(x_{41}\)	\(x_{42}\)	\(x_{43}\)

\(x_{ij}\): weight of cargo of type \(i\) in position \(i\) in the airplane with \( i \in 1,2,3,4\) and \( j \in 1,2,3 \) Note: you can use as unit of the variables the volume too but in that case the constraints are going to be slightly different

Objective

If we define \(P_i\) as the profit obtained for one ton of cargo of type \( i \in 1,2,3,4\) then the objective function is to maximize the profit:

\[\max \left( Z \right) = \sum\limits_{i = 1}^4 {\sum\limits_{j = 1}^3 {{P_i}{x_{ij}}} } \]

\[{P_i} = \left[ {590}, {580}, {580}, {600} \right]\]

Constraints

Weight available to be transported at the warehouses:

\[\begin{split} \begin{align*} {x_{11}} + {x_{12}} + {x_{13}} \le 18 \\ {x_{21}} + {x_{22}} + {x_{23}} \le 14 \\ {x_{31}} + {x_{32}} + {x_{33}} \le 20 \\ {x_{41}} + {x_{42}} + {x_{43}} \le 12 \end{align*}\end{split}\]

Weight limits on the compartments:

\[\begin{split}\begin{align*} {x_{11}} + {x_{21}} + {x_{31}} + {x_{41}} \le 8 \\ {x_{12}} + {x_{22}} + {x_{32}} + {x_{42}} \le 12 \\ {x_{13}} + {x_{23}} + {x_{33}} + {x_{43}} \le 14 \end{align*}\end{split}\]

Volume limits on the compartments:

\[\begin{split}\begin{align*}180{x_{11}} + 250{x_{21}} + 300{x_{31}} + 80{x_{41}} \le 12000 \\ 180{x_{12}} + 250{x_{22}} + 300{x_{32}} + 80{x_{42}} \le 10000 \\ 180{x_{13}} + 250{x_{23}} + 300{x_{33}} + 80{x_{43}} \le 6000 \end{align*}\end{split}\]

Variables domain

\[{x_{ij}} \ge 0\]

Task 2

Model the problem in Python using Gurobi.

Solution

The implementation is shown here.

Task 3

Task 4

What is the distribution of cargo for the optimal solution?

Solution

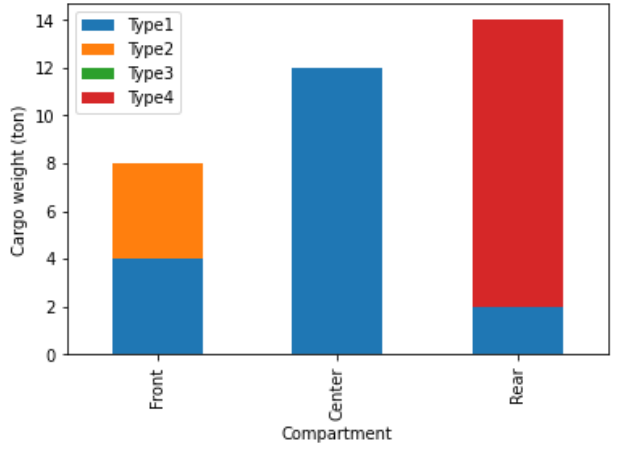
Fig. 5.32 Distribution airplane problem

Challenges

Challenge 1

For efficiency purposes, the total weight transported in all compartments must be the same.

Task 1

How do you change the model?

Solution

Additional constraints:

\[\begin{split}\begin{align*} {x_{11}} + {x_{21}} + {x_{31}} + {x_{41}} = {x_{12}} + {x_{22}} + {x_{32}} + {x_{42}} \\ {x_{12}} + {x_{22}} + {x_{32}} + {x_{42}} = {x_{13}} + {x_{23}} + {x_{33}} + {x_{43}} \end{align*}\end{split}\]

Task 2

Task 3

What is the distribution of cargo for the optimal solution?

Solution

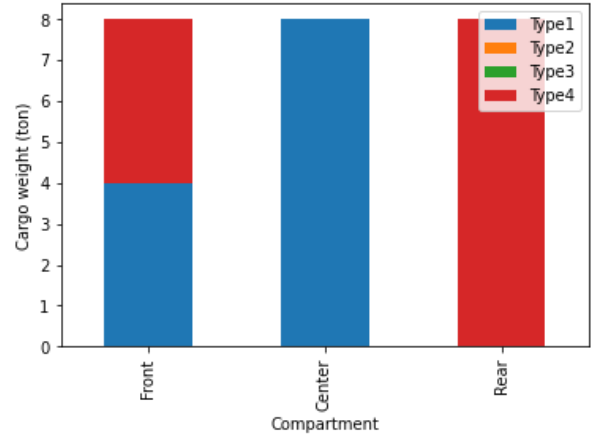
Fig. 5.33 Distribution airplane problem challenge 1

Challenge 2

The weight of type I must be double the Type II and III together.

Task 1

How do you change the model?

Solution

Additional constraint:

\[{x_{11}} + {x_{12}} + {x_{13}} = 2\left( {{x_{21}} + {x_{22}} + {x_{23}}} \right) + 2\left( {{x_{31}} + {x_{32}} + {x_{33}}} \right)\]

Task 2

Task 3

What is the distribution of cargo for the optimal solution?

Solution

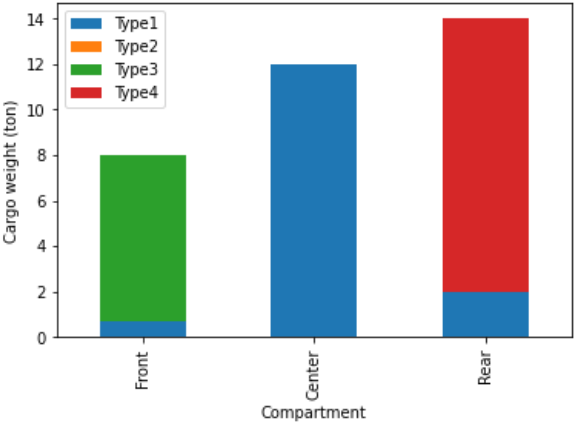
Fig. 5.34 Distribution airplane problem challenge 2

Challenge 3:

The weight of cargo in the frontal area must be at least double the cargo in the rear and central areas together.

Task 1

How do you change the model?

Solution

Additional constraint:

\[{x_{11}} + {x_{21}} + {x_{31}} + {x_{41}} \ge 2\left( {{x_{12}} + {x_{22}} + {x_{32}} + {x_{42}}} \right) + 2\left( {{x_{13}} + {x_{23}} + {x_{33}} + {x_{43}}} \right)\]

Task 2

Task 3

What is the distribution of cargo for the optimal solution?

Solution

Fig. 5.35 Distribution airplane problem challenge 3

Attribution

This chapter is written by Gonçalo Homem de Almeida Correia, Maria Nogal Macho, Jie Gao and Bahman Ahmadi. Find out more here.