1.2. Model decisions#
In this section, we are going to focus on the decisions we make when setting up a model. We will start seeing models as part of the creative and decision making process!
When building a model, we need to identify which simplifications we can make to keep our model as simple as possible, while modelling the system we are interested in with the appropriate accuracy. In real-life applications, simpler models also equates to lower costs, so it is often one of the main considerations in model design. In short, the simpler, the better, as long as it answers our questions. We are going to talk about the following characteristics of a model:
Dynamic vs. static models
Linear vs. non-linear models
Time-invariant vs. Time-variant models
Deterministic vs. Stochastic models
Dynamic vs. Static#
The decision between dynamic and static models is based on whether a model needs to account for previous or future states. In other words, the response of a dynamic model will have a dependence on the past and future states of the system. On the contrary, in a static model, we consider the response of the system only depending on present values and, thus, the model does not account for previous time steps.
Let’s see an example.
In classical mechanics, as you know, motion is governed by Newton’s laws - the second law in particular - that allow us to write the famous main equation of motion that we have know for years:
Let us consider the mass-spring system as a first example.
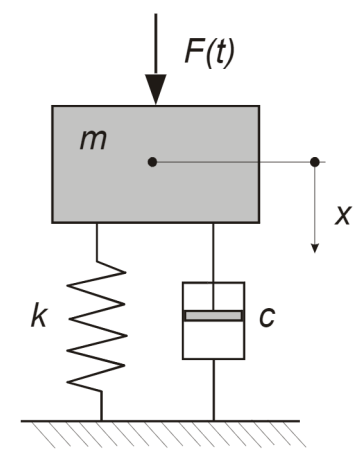
Fig. 1.4 Mass-spring system.#
For this system, Newton’s equations of motion sketch as:
In this equation, a dependence exists between the present and past states of the system. Thus, it is a dynamic model. This equation can be tricky to solve: it is both dynamic and nonlinear (see below)… However, it is also possible to simplify it!
If the terms with the derivatives are small and negligible when compared to \(x\), then we find the following equation of motion:
Under which circumstances does this occur?
Slow loading rate: constant \(F\) or \(F\cos(\omega t)\) if \(\omega<\omega_0\), where \(\omega_0\) is the natural frequency of the system
Small mass and small values of the damping constant, \(c\)
In those circumstances, we can make the assumption that the model is static (simplification) and still get accurate answers to our questions using the simplified model.
Linear vs Nonlinear#
In linear models, the relationships between variables can be modelled using linear predictor functions. One advantage of these models is that the superposition principle applies and the long term behavior does not depend on initial conditions. On the contrary, in non-linear models, the superposition principle does not apply anymore and long and short term behavior is highly dependent on the initial conditions.
Let’s see an example.
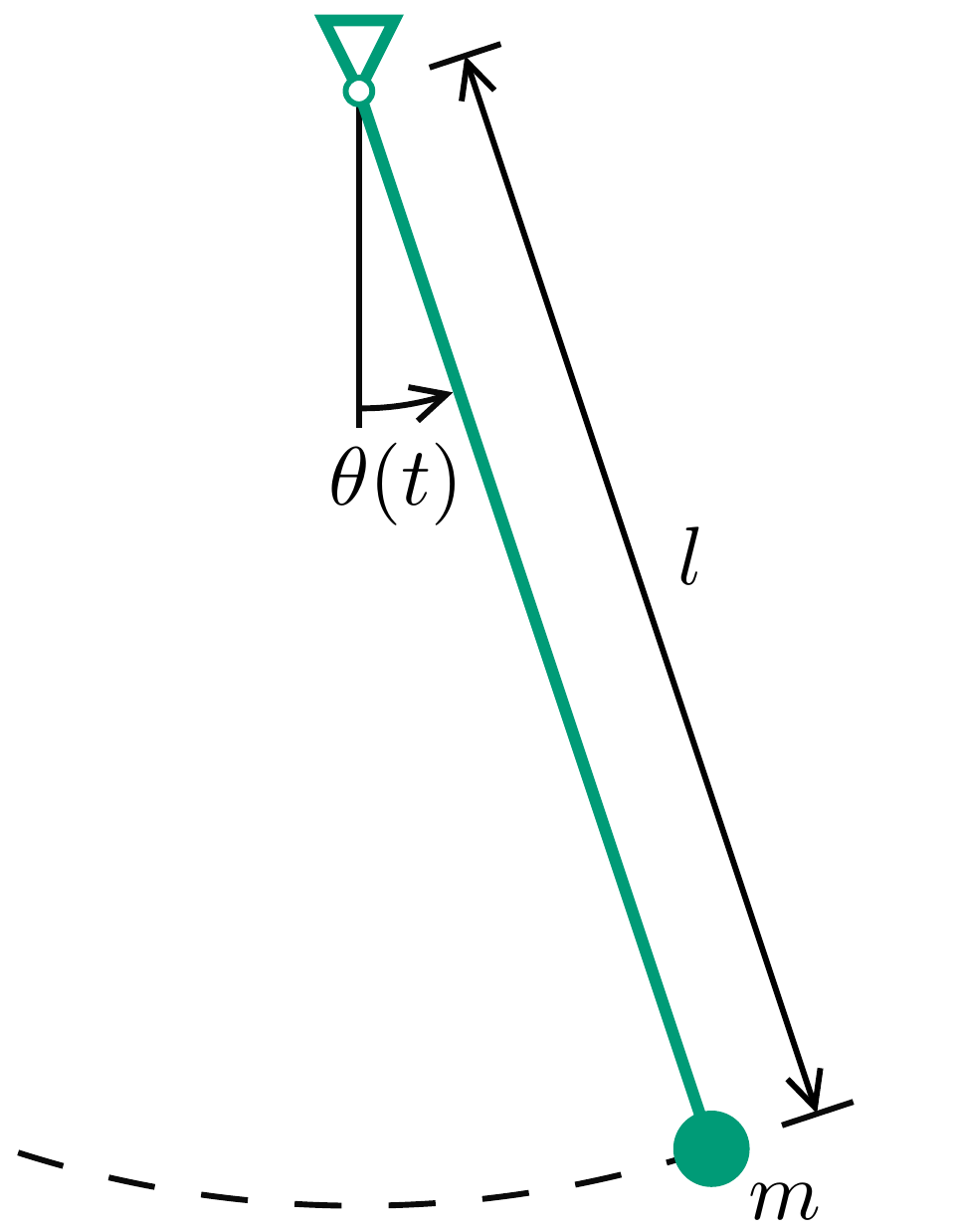
Fig. 1.5 Classical pendulum as illustration for linearization#
Let us consider a classical physics example: the simple pendulum. The force acting on the mass depends nonlinearly on its position, making Newton’s equations give rise to a nonlinear differential equation:
However… this equation can be linearized around \(\theta=0\), using \(\sin\theta \approx \theta\). This assumption is reasonable when the motion of the pendulum is small compared to the length of the pendulum. Then, the equation of motion becomes a linear differential equation:
Very often this linearized version of the equation is used for analyzing the pendulum problem and similar simplifications are routinely made for different physical systems. Linearization generally comes with loss of accuracy, but under given circumstances this loss may remain limited, and then the simplified analysis options that a linear model offers are very appealing.
Time-invariant vs Time-variant#
In time-invariant models, the model coefficients or model parameters are constant. This is, the response or properties of the system do not change over time. In time-variant models, the model parameter do change over time, so the behavior of the system evolves.
And how do I choose between a time-variant and time-invariant model?
Mainly based on the knowledge I have about the system! As an engineer, I will have to assess whether or not such changes are relevent for my problem. For instance, nowadays, we consider climate change when designing a breakwater. It has been proved that waves and storms are becoming more extreme over time. I will have to account for this to assess the performance of the breakwater. However, if I am designing a temporary platform to assist in some construction works in the sea, I will not take it into account. Climate change is a long-time scale process. It will impact on the life cycle of a breakwater which is meant to be there for tens or even hundreds of years. On the other hand, the influence of climate change on a platform that will only be there for a few weeks is negligible.
Deterministic vs Stochastic#
Deterministic models are those which for some given inputs, always provide the same output. For instance, a equation which gives the average concentration of \(\text{CO}_2\) in a city as function of the traffic. For a certain value of traffic, the model will always provide the same concentration of \(\text{CO}_2\). In these models, there is no uncertainty (other than the uncertainty of the input data). Stochastic models embrace the uncertainty. This is, stochastic models will produce different outputs for a given input. In fact, the inputs and outputs of stochastic models are probabilistic distributions (you will learn more about this later!), which relate the values of the variable with the probability of observing it.
And how do I choose between a deterministic and stochastic model?
All systems in reality are stochastic, since we never truly know the actual properties and inputs. However, under certain circumstances, this stochasticity can be neglected. Let us take a look to some examples of deterministic and stochastic systems:
Cases of stochastic systems:
Structures or systems with known or unknown properties subject to unknown or known loads, respectively:
Soil systems: we can extract samples of soil but we cannot see or measure the properties of every point in the system.
Traffic systems: inputs are too complicated, from weather to human decisions.
Note that there are also uncertainties regarding the measurement of the observations (you will also learn about this later!).
Cases of deterministic systems:
Known structures subject to known static or dynamic loads. For instance, when we decide to model the response of a building (deformations) under a specific (known) load. Note, however, that in practice loads are almost always variable, or impossible to predict with certainty; thus we will often use deterministic models to understand the behavior of the structure of interest, while also using a stochastic models to check whether the structure will perform well under the range of loads that can be expected.
Attribution
This chapter was written by Alessandro Cabboi, Patricia Mares Nasarre and Robert Lanzafame. Find out more here.
