Matrix and vector manipulations

import numpy as np
import matplotlib.pyplot as plt

In some cases, matrices and vectors are composed of sub-matrices or sub-vectors. In another cases we may want to ‘reshape’ a matrix, or reshape a vector into a matrix, or vice versa. We can conveniently do such operations using some standard numpy functions:

• np.block to create a matrix from sub-matrices

• np.concatenate to combine two or more vectors into one vector

• np.reshape to change the shape of a matrix

Let’s go over a some exercises to see how to manipulate matrices and vectors using these functions.

\(\text{Task 3.1:}\)

Run the code below to create four different matrices and combine these into a single matrix.

Complete the code to extract the top row of matrix A1 into vector b1 and the top row of matrix A2 into vector b2.

A11 = np.array([
    [1, 0, 0, 0, 1, 0],
    [1, 1, 0, 1, 1, 0],
    [1, 0, 1, 0, 1, 0],
    [1, 0, 0, 0, 1, 0],
    [1, 0, 0, 0, 1, 0],
    [0, 0, 0, 0, 0, 0]])

A12 = np.array([
    [1, 0, 0, 0, 1],
    [1, 0, 0, 0, 1],
    [1, 0, 0, 0, 1],
    [1, 0, 0, 0, 1],
    [0, 1, 1, 1, 0],
    [0, 0, 0, 0, 0]])

A21 = A12.transpose().copy()
A21[1:4,0] = 1

A22 = np.array([
    [1, 1, 1, 1, 1],
    [1, 0, 0, 0, 0],
    [1, 1, 1, 1, 1],
    [1, 0, 0, 0, 0],
    [1, 1, 1, 1, 1]])

b1 = A11[0,:]
b2 = A12[0,:]

\(\text{Task 3.2:}\)

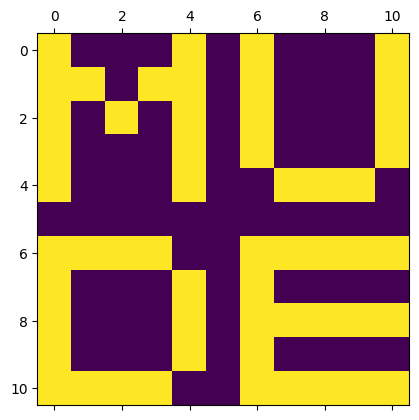
Run the code below to create a single matrix A from the four sub-matrices and combine the two b-vectors into a single vector b. Print vector b and plot matrix A using plt.matshow.

A = np.block([[A11, A12],
              [A21, A22]])

b = np.concatenate([b1, b2])

print(b)
plt.matshow(A)
plt.show()

[1 0 0 0 1 0 1 0 0 0 1]

Now, we will use the np.reshape function to change the shape of a matrix.

Reshape puts all matrix components row-by-row behind each other in a long vector and then recreates the matrix according to the new shape by taking row-by-row from the long vector.

\(\text{Task 3.3:}\)

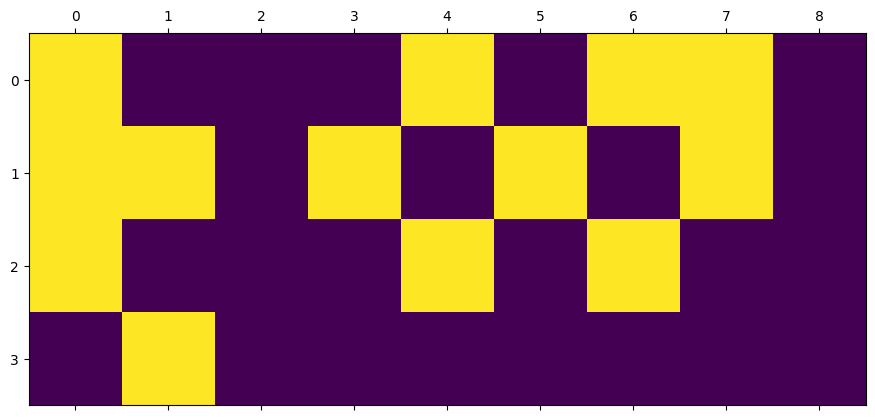
Run the code below to change the shape of the matrix A11 and A21, and plot the resuls using plt.matshow.

A11 = A11.reshape(4,9)
plt.matshow(A11)
A21 = A21.reshape(6,5)
plt.matshow(A21)
plt.show()

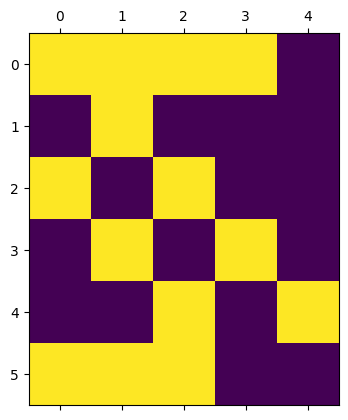
Note that the results look quite different than the original (sub-)matrices, and the operation seems quite useless. Nevertheless, in some situations it might be useful to perform operations on a vector and reshape the result back into matrix, as we will see later on in MUDE.

\(\text{Task 3.4:}\)

Play with the reshape function yourself. Note that the total number of elements in the original matrix and the reshaped matrix must remain equal.

By Ronald Brinkgreve, Delft University of Technology. CC BY 4.0, more info on the Credits page of Workbook.