# Matplotlib compatibility patch for Pyodide
import matplotlib
if not hasattr(matplotlib.RcParams, "_get"):
    matplotlib.RcParams._get = dict.get

1.4. Advection-diffusion equation

In Sections Diffusion Equation and Advection Equation we have treated the numerical solution of the diffusion equation and the advection equation, respectively. By combining these processes we obtain the following 1D advection-diffusion equation

(1.21)\[ \frac{\partial c}{\partial t} + u\frac{\partial c}{\partial x} - \kappa\frac{\partial^2 c}{\partial x^2} = 0 \]

This instationary advection-diffusion equation describes the time evolution of a constituent \(c(x,t)\) that is transported with flow velocity \(u\) and at the same time diffuses (or spreads) with a diffusion coefficient \(\kappa\). This PDE is classified as a parabolic one.

In some cases, however, we may be interested in the steady state only. In this respect, the following stationary equation will be considered

(1.22)\[ u\frac{dc}{dx} - \kappa\frac{d^2 c}{dx^2} = 0 \]

which renders the balance between advection and diffusion.

Note

Eq. (1.21) is a 1D PDE while Eq. (1.22) is a 1D ODE. However, a 2D stationary advection-diffusion equation as given by

\[ u\frac{\partial c}{\partial x} + v\frac{\partial c}{\partial y} - \kappa \left ( \frac{\partial^2 c}{\partial x^2} + \frac{\partial^2 c}{\partial y^2} \right ) = 0 \]

is an elliptic PDE. Here, \(v\) is the flow velocity in \(y-\)direction.

We first deal with the numerical solution of the stationary advection-diffusion equation (1.22) and then that of instationary advection-diffusion equation (1.21) in separate sections. In particular we dive into the role and the meaning of central differences and the first order upwind scheme with respect to the numerical solution of the particular PDE. In this context, we will explore the phenomena like wiggles and numerical diffusion. Such phenomena are called numerical artifacts and have no corresponding property in the real world. Wiggles are caused by central differences and numerical diffusion is typically created by the first order upwind scheme. In this section, we will explore how to reduce wiggles through diffusion, either physical and/or numerical.

Note

The learning objectives of this section are:

• formulate and discretize the advection-diffusion equation using central differences and the first order upwind scheme

• explain the notions of wiggles and numerical diffusion

• describe the role of the mesh Péclet number

• discuss the possibilities to reduce wiggles

Stationary advection-diffusion equation

The following 1D boundary value problem is considered

(1.23)\[\begin{split} \begin{align} &u\frac{dc}{dx} - \kappa\frac{d^2c}{dx^2} = 0\, , \quad 0 < x < 1 \\ & \\ &c(0) = 0 \\ & \\ &c(1) = 1 \end{align} \end{split}\]

The solution to this BVP is the spatial distribution of the constituent \(c(x)\) along the interval \(0 \leq x \leq 1\) as depicted below.

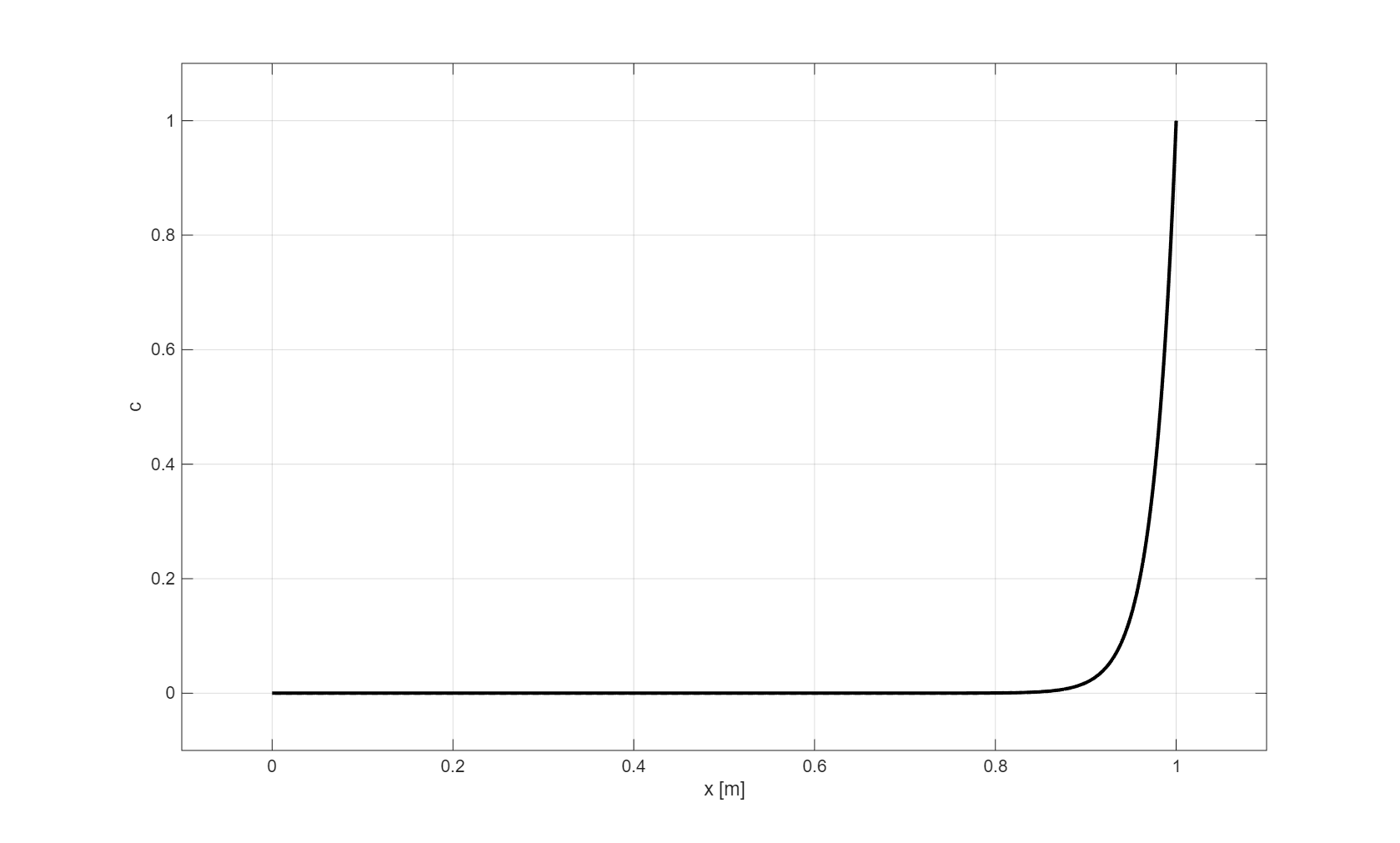
Fig. 1.8 Exact solution to Eq. (1.23) with \(\kappa = 0.025\) m\(^2\)/s and \(u = 1\) m/s.

Generally, this constituent \(c(x)\) is assumed to be smooth enough. Clearly, the solution displays a steep gradient in the boundary layer. The thickness of this layer is mainly determined by the amount of diffusion involved and is due to the fact that the solution has to match to all the given boundary conditions. The boundary layer thickness is proportional to the square root of \(\kappa\). To accurately solve this boundary layer, a local mesh refinement is often necessary.

Based on accuracy reasons, we choose central differences for both advective and diffusive processes, as follows

(1.24)\[ u\frac{c_{m+1}-c_{m-1}}{2\Delta x} - \kappa \frac{c_{m+1}-2c_m+c_{m-1}}{\Delta x^2} = 0\, , \quad m = 1,\ldots,M-1 \]

Exercise

Verify this approximation and show that \(\tau_{\Delta x} = \mathcal{O}(\Delta x^2)\).

The boundary conditions are simply discretized as follows

\[ c_0 = 0 \, , \quad c_M = 1 \]

A peculiar feature of central differences applied to the first derivative \(\partial c/\partial x\) (or generally, the advection term) is that they are prone to generate spurious oscillations or wiggles, especially near steep gradients, see for example Fig. 1.9. This renders the numerical solution physically meaningless. The way to counteract these wiggles is to add some diffusion. The effect of this diffusion process is to smear out these irregularities. The question arises whether the amount of physical diffusion, as indicated by \(\kappa\), is considered to be enough to prevent oscillations. To answer this question, we rewrite Eq. (1.24) as follows

(1.25)\[ \left ( \frac 12 P_{\Delta} - 1 \right ) c_{m+1} + 2c_m - \left ( \frac 12 P_{\Delta} + 1 \right ) c_{m-1} = 0 \]

with

\[ P_{\Delta} = \frac{u\Delta x}{\kappa} \]

the so-called mesh Péclet number.

Note that because of consistency, the sum of the coefficients of Eq. (1.25) is zero. Hence, with \(p=\)½\(P_{\Delta}-1\) and \(q=-\)½\(P_{\Delta} - 1\), we have \(p+q+2=0\). Eq. (1.25) represents a recurrent relation of second order and its general solution is of the form

\[ c_m = \alpha\, r_1^m + \beta\, r_2^m \]

where \(\alpha\) and \(\beta\) are some constants and \(r_1\) and \(r_2\) are the roots of the following characteristic equation

\[ r^2 - \left ( 1 + \frac{q}{p} \right ) r + \frac{q}{p} = 0 \]

These roots are given by

\[ r_1 = 1\, , \quad r_2 = \frac{q}{p} = \frac{2+P_{\Delta}}{2-P_{\Delta}} \]

Exercise

Verify the above characteristic equation and its roots.

Solution

From Eq. (1.25) we have the following

\[ p\, c_{m+1} - (p+q)\, c_m + q\, c_{m-1} = 0 \]

or

\[ c_{m+1} - \left ( 1 + \frac{q}{p} \right ) c_m + \frac{q}{p} c_{m-1} = 0 \]

The associated characteristic equation is then given by

\[ r^2 - \left ( 1 + \frac{q}{p} \right ) r + \frac{q}{p} = 0 \]

This is a quadratic equation for which the two roots can be found as

\[ r_{1,2} = \frac{p+q \pm \sqrt{p^2+q^2 -2pq}}{2p} \]

or

\[ r_1 = 1\, , \quad r_2 = \frac{q}{p} \]

To prevent wiggles, both roots must be non-negative.

Why?

To see why this is so, we consider the solution

\[ c_m = r^m \]

This implies that

\[ c_{m+1} = r^{m+1} = r \times r^m = r\,c_m \quad \Rightarrow \quad r = \frac{c_{m+1}}{c_m} \]

Hence, if both solutions \(c_m\) and \(c_{m+1}\) are positive (or negative) then \(r > 0\). However, if \(c_m>0\) but the next one \(c_{m+1} <0\) (or the other way around), thus the solution oscillates, then \(r<0\). Therefore, wiggles in the solution occur as soon as \(r<0\).

Here, we must require \(r_2 \geq 0\). Hence, the restriction on the mesh Péclet number reads

(1.26)\[ |P_{\Delta}| = \frac{|u|\Delta x}{\kappa} \leq 2 \]

Exercise

Derive this restriction.

Solution

The second root \(r_2\) must be non-negative which implies

\[ \frac{2+P_{\Delta}}{2-P_{\Delta}} \geq 0 \]

There are two possibilities:

• both numerator \(2+P_{\Delta}\) and denominator \(2-P_{\Delta}\) are positive

• both numerator \(2+P_{\Delta}\) and denominator \(2-P_{\Delta}\) are negative

The first possibility provides the appropriate restriction, namely,

\[ -2 \leq P_{\Delta} \leq 2 \]

while the second possibility yields

\[ P_{\Delta} < -2 \quad \text{and} \quad P_{\Delta} > 2 \]

which is not possible.

Let us consider our example with \(\kappa=0.025\) m\(^2\)/s and \(u=1\) m/s and we choose \(\Delta x = 0.1\) m, so that \(P_{\Delta} = 4\). The following figure depicts the obtained numerical solution that clearly shows wiggles \(-\) the solution oscillates around the boundary layer. In this case, \(P_{\Delta} > 2\) which implies that the current amount of physical diffusion is not sufficient to prevent wiggles.

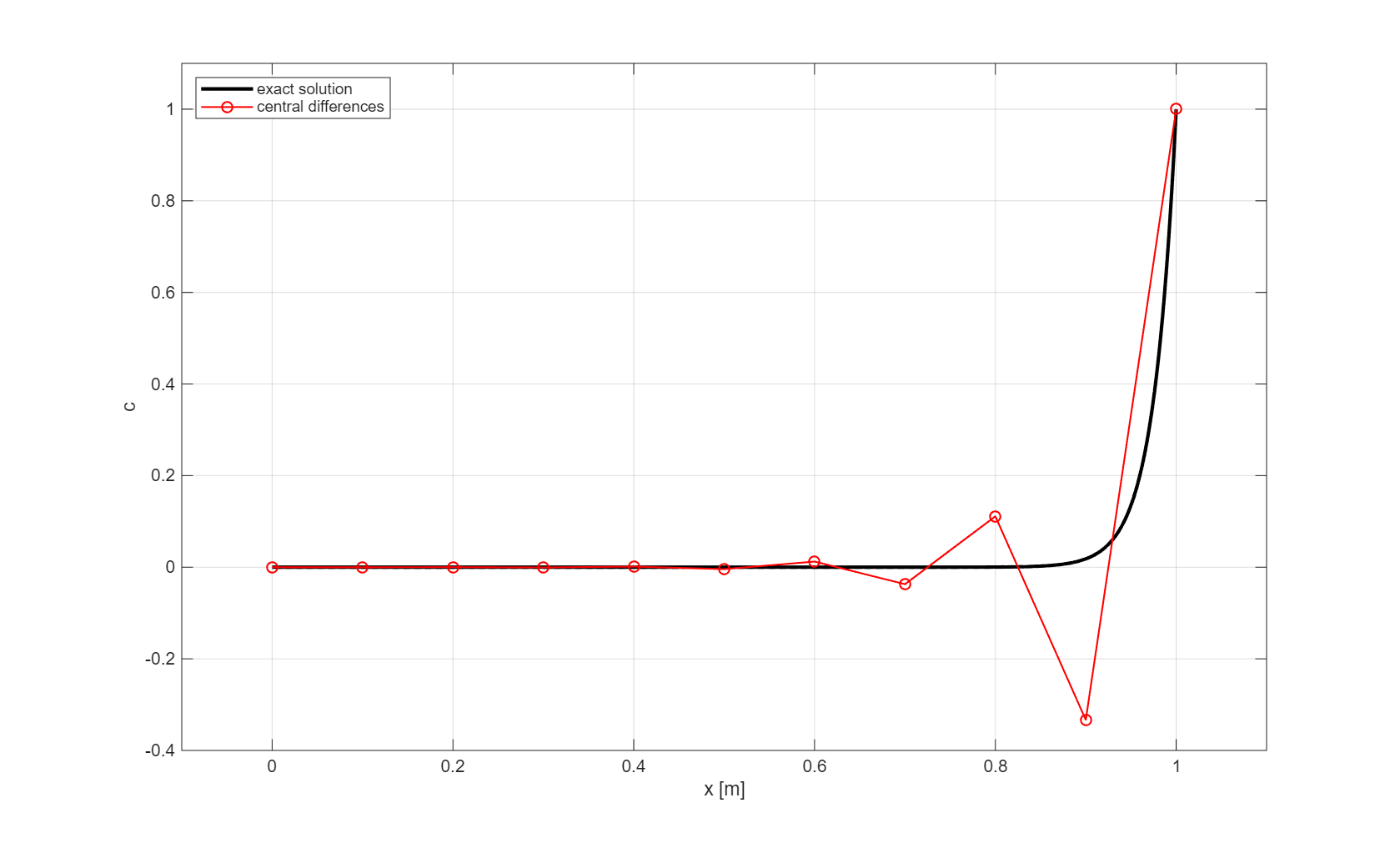
Fig. 1.9 Solution obtained with central differences and \(\Delta x = 0.1\) m.

A simple remedy would be to decrease the mesh size \(\Delta x\) such that restriction (1.26) is fulfilled. This is demonstrated with the following example. We now choose \(\Delta x = 0.025\) m, so that \(P_{\Delta} = 1\). The result is depicted in the following figure.

Fig. 1.10 Solution obtained with central differences and \(\Delta x = 0.025\) m.

Exercise

Let the velocity and diffusion coefficient still be given as \(u = 1\) m/s and \(\kappa = 0.025\) m\(^2\)/s, respectively. What is the maximum mesh size \(\Delta x\) for the numerical solution to be wiggle-free?

You can try it out yourself with the slider below. (Note: the parameter Nx represents the number of grid cells contained in the domain \(x \in [0,1]\).)

import numpy as np
import matplotlib.pyplot as plt
from ipywidgets import interact, widgets

def central(M):
    a=0
    b=1
    u=1
    e=0.025
    #
    # exact solution of boundary layer
    xe = np.arange(0, 1.001, 0.001)
    t=a+(b-a)*(1-np.exp(u*xe/e))/(1-np.exp(u/e))
    #
    # central differences
    if M == 0:
        h=1.
    else:
        h=1/M
    q=u*h/(2*e)
    r=(1+q+0.00000001)/(1-q-0.00000001)
    x = np.arange(0, 1+h, h)
    k = np.arange(0, M+1, 1)
    if M == 0:
        k=np.arange(0, 2, 1)
        d=np.zeros(len(k))
        maxp=1.2
    else:
        d=a+(b-a)*(1-r**k)/(1-r**M)
        maxp=0.2
    #
    # plot results
    fig = plt.figure()
    ax = plt.axes(xlim=(-0.1, 1.1), ylim=(d.min()-0.2, d.max()+maxp))  
    ax.plot(xe,t,label='exact solution',color="black")
    ax.plot(x[0:len(k)],d,label='numerical solution',color="red",marker="o")
    ax.legend()
    plt.xlabel('x [m]')
    plt.ylabel('c')
    plt.title(f"central differences with dx = {h}")
    plt.show()

# create an interactive slider
interact(
    central,
    M=widgets.IntSlider(value=1, min=1, max=100, step=1, description="Nx"),
);

In practice, this increase of mesh resolution can be a severe one. Another remedy would be to apply the first order upwind scheme. This is explained in the following way.

In general, numerical diffusion arises from a first order finite difference scheme to the spatial derivative \(\partial c/\partial x\). To see this why this is so, recall the Taylor series expansion of \(c(x_{m+1})\):

\[ c(x_{m+1}) = c(x_m) + \Delta x\, \frac{\partial c}{\partial x}(x_m) + \frac 12 \Delta x^2\, \frac{\partial^2 c}{\partial x^2}(x_m) + \text{ HOT} \]

where HOT stands for higher order terms. Now the first derivative at point \(x_m\) can be written as

\[ \frac{\partial c}{\partial x} = \frac{c(x_{m+1}) - c(x_m)}{\Delta x} - \frac 12 \Delta x\, \frac{\partial^2 c}{\partial x^2} + \text{ HOT} \]

Here, we have expressed the exact first derivative by the first order forward difference formula plus higher order terms.

Now, let us consider the following advection equation at point \(x_m\):

\[ \frac{\partial c}{\partial t}(x_m) + u\frac{\partial c}{\partial x}(x_m) = 0 \]

and then replace the first derivative by the first order differences above while moving the higher order terms to the right hand side, as follows

\[ \frac{\partial c}{\partial t}(x_m) + u\frac{c(x_{m+1}) - c(x_m)}{\Delta x} - \kappa_a \, \frac{\partial^2 c}{\partial x^2}(x_m) = \text{HOT} \]

where

\[ \kappa_a = \frac{u\,\Delta x}{2} \]

is the diffusion coefficient associated with the first order differences. This amount of diffusion has no physical meaning and is therefore called numerical diffusion.

We conclude that the original diffusion-free PDE has been converted into an advection-diffusion PDE due to truncation error. Since the amount of numerical diffusion \(\kappa_a\) is proportional to \(\Delta x\), this amount cannot be neglected, that is, the term \(\kappa_a c_{xx}\) cannot be considered as a negligible truncation error.

Below we will demonstrate that the first order upwind scheme generates sufficient amount of numerical diffusion so that wiggles are prevented. Let us assume \(u>0\). Hence, we have the following discretized equation for internal points \(m = 1,\cdots,M-1\),

(1.27)\[ u\frac{c_m-c_{m-1}}{\Delta x} - \kappa \frac{c_{m+1}-2c_m+c_{m-1}}{\Delta x^2} = 0 \]

Exercise

Verify this approximation and show that \(\tau_{\Delta x} = \mathcal{O}(\Delta x)\).

The corresponding characteristic equation is given by

\[ r^2 - (P_{\Delta} +2) \, r + P_{\Delta}+1 = 0 \]

and its roots are

\[ r_1 = 1\, , \quad r_2 = 1+P_{\Delta} \]

Hence, both roots are always non-negative (\(P_{\Delta}>0\), since \(u>0\)) and the numerical solution will not display any oscillations, irrespective of the value of \(P_{\Delta}\).

Precautions should be taken so that the numerical diffusion will not dominate the physical one, that is, \(\kappa_a < \kappa\). Otherwise, the first order upwind scheme is considered to be too dissipative. In practice, this means mesh refinement if desired.

Exercise

Let us recall the above example with \(u = 1\) m/s, \(\kappa = 0.025\) m\(^2\)/s and let \(\Delta x = 0.1\) m. Next, we consider the first order upwind scheme as given above.

What is \(P_{\Delta}\)? And how much is the amount of numerical diffusion \(\kappa_a\)? Compare this amount with the physical one and use the slider below to see what the solution looks like. What can you conclude regarding the boundary layer thickness?

Now, let us see what happen if we refine the grid four times. Answer the questions above and use the slider if necessary.

import numpy as np
import matplotlib.pyplot as plt
from ipywidgets import interact, widgets

def upwind(M):
    a=0
    b=1
    u=1
    e=0.025
    #
    # exact solution of boundary layer
    xe = np.arange(0, 1.001, 0.001)
    t=a+(b-a)*(1-np.exp(u*xe/e))/(1-np.exp(u/e))
    #
    # first order upwind scheme
    if M == 0:
        h=1.
    else:
        h=1/M
    e=e+0.5*u*h
    q=u*h/(2*e)
    r=(1+q)/(1-q)
    x = np.arange(0, 1+h, h)
    k = np.arange(0, M+1, 1)
    if M == 0:
        k=np.arange(0, 2, 1)
        d=np.zeros(len(k))
    else:
        d=a+(b-a)*(1-r**k)/(1-r**M)
    #
    # plot results
    fig = plt.figure()
    ax = plt.axes(xlim=(-0.1, 1.1), ylim=(-0.1, 1.1))  
    ax.plot(xe,t,label='exact solution',color="black")
    ax.plot(x[0:len(k)],d,label='numerical solution',color="red",marker="o")
    ax.legend()
    plt.xlabel('x [m]')
    plt.ylabel('c')
    plt.title(f"upwind scheme with dx = {h}")
    plt.show()

# create an interactive slider
interact(
    upwind,
    M=widgets.IntSlider(value=1, min=1, max=100, step=1, description="Nx"),
);

Solution

With \(\Delta x = 0.1\) m, we find \(P_{\Delta} = 4\). Furthermore, the amount of numerical diffusion equals \(\kappa_a = 0.5 \times 1 \times 0.1 = 0.05\) m\(^2\)/s which is twice larger than the physical one. The corresponding numerical solution is depicted below which shows that it is rather inaccurate. Note that the boundary layer thickness of the numerical solution is larger than that of the exact one due to numerical diffusion.

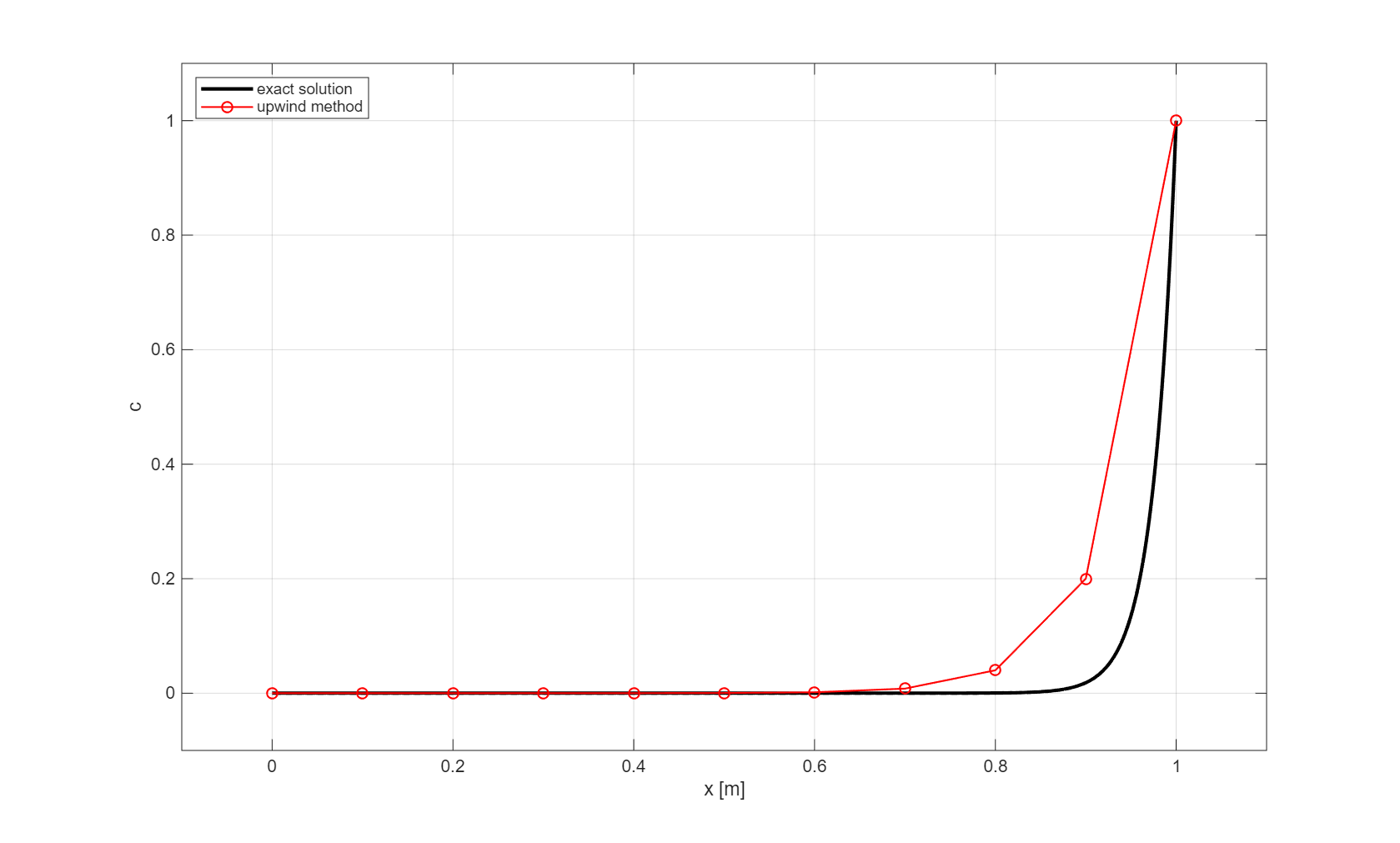
Fig. 1.11 Solution obtained with the first order upwind scheme and \(\Delta x = 0.1\) m so that \(\kappa_a = 0.05\) m\(^2\)/s.

Now, let us see what happen if we refine the grid four times, so that \(\Delta x = 0.025\) m. Hence, \(\kappa_a = 0.0125 < \kappa = 0.025\) m\(^2\)/s. The numerical solution is plotted below.

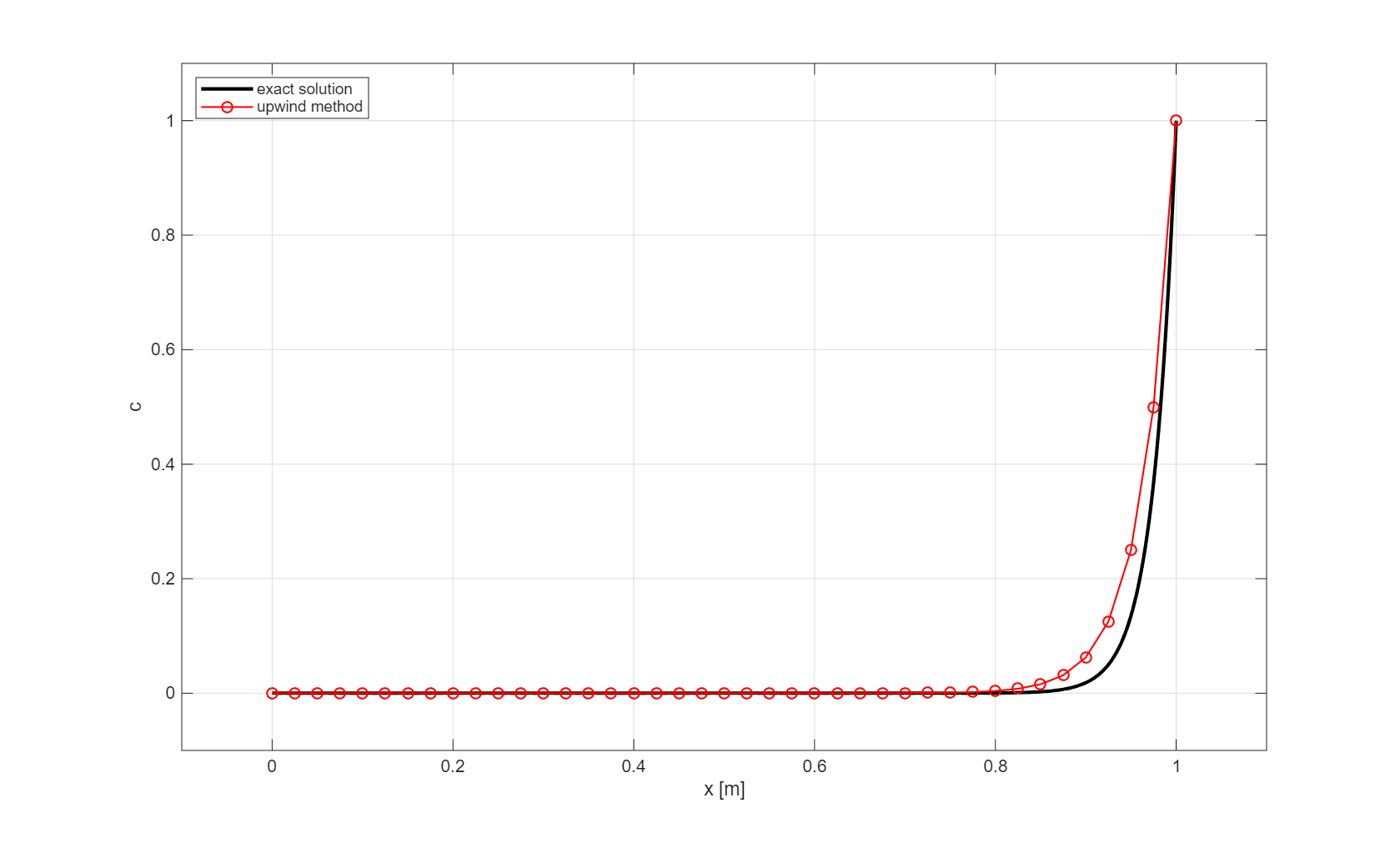
Fig. 1.12 Solution obtained with the first order upwind scheme and \(\Delta x = 0.025\) m.

Accuracy

Let us explore the accuracy of the first order upwind scheme (1.27) and the second order central differences (1.24). First, use the slider of central differences and determine how many grid cells you need so that there is no visual difference between the numerical solution and the exact solution.

Then, using the slider of the upwind scheme, set the number of cells you just determined and then compare the corresponding numerical solution with that of the solution of central differences.

What do you observe?

Solution

The solution obtained with the first order upwind scheme is less accurate compared to central differences. This is explained by the fact that scheme (1.27) is first order accurate, so that the numerical solution converges more slowly to the exact solution compared to the second order central difference scheme (1.24).

We may perhaps conclude that it is wiser to prefer central differences over the first order upwind scheme provided the grid is sufficiently fine, at least for linear advection-diffusion equations. In practice, however, we see that upwind schemes are a much more robust alternative for nonlinear problems (such as the Navier-Stokes or shallow water equations) despite being generally less accurate.

Instationary advection-diffusion equation

We consider the following 1D initial boundary value problem

(1.28)\[\begin{split} \begin{align} &\frac{\partial c}{\partial t} + u\frac{\partial c}{\partial x} - \kappa\frac{\partial^2 c}{\partial x^2} = 0\, , \quad 0 < x < 1 \, , \quad t > 0 \\ &\\ &c(x,0) = 0\, , \quad 0 \leq x \leq 1 \\ &\\ &c(0,t) = 0\, , \quad t > 0 \\ &\\ &c(1,t) = 1\, , \quad t > 0 \end{align} \end{split}\]

Again, we assume that the constituent \(c(x,t)\) is sufficiently smooth. The solution to this problem is called transient and in the limit, \(t \to \infty\), a steady state solution may be obtained. This is the case when the boundary conditions are time independent. This is also the solution to the stationary problem (1.23).

For the discretization of (1.28), we employ the method of lines. First, we apply second order central differences to spatial derivatives. The semi-discretized equation reads

\[ \frac{dc_m}{dt} + u\frac{c_{m+1}-c_{m-1}}{2\Delta x} - \kappa \frac{c_{m+1}-2c_m+c_{m-1}}{\Delta x^2} = 0\, , \quad m = 1,\ldots,M-1\, , \quad t > 0 \]

A commonly time integration method would be the forward Euler method. Thus, we obtain the following discretized equation for the instationary advection-diffusion equation (1.28),

(1.29)\[ \frac{c^{n+1}_m-c^n_m}{\Delta t} + u\frac{c^n_{m+1}-c^n_{m-1}}{2\Delta x} - \kappa \frac{c^n_{m+1}-2c^n_m+c^n_{m-1}}{\Delta x^2} = 0\, , \quad m = 1,\ldots,M-1\, , \quad n=0,1,2,\ldots \]

This scheme is first order accurate in time but second order in space. Furthermore, it is explicit and thus conditionally stable. By requiring non-negative solutions we may find some stability conditions. We rewrite the discretized equation as

\[ c^{n+1}_m = (q - \frac 12 \sigma) c^n_{m+1} + (1-2q) c^n_m + (q + \frac 12 \sigma) c^n_{m-1} \]

with \(q = \kappa \,\Delta t/\Delta x^2\) and \(\sigma = u\,\Delta t/\Delta x\).

and by induction, we assume that \(c^n_m \geq 0\) for \(m=0,\ldots,M\). To have \(c^{n+1}_m \geq 0\), the following conditions must be met

\[ \boxed{ q \leq \frac 12 \, , \quad |P_{\Delta}| \leq 2 } \]

Exercise

Verify these conditions.

Solution

First, we rewrite (1.29) to express the unknown at the new time step \(n+1\) into the unknowns at the present time step \(n\), using the numerical parameters \(q\) and \(\sigma\), as follows

\[ c^{n+1}_m = c^n_m - \frac 12 \sigma \left (c^n_{m+1}-c^n_{m-1} \right) + q \left( c^n_{m+1}-2c^n_m+c^n_{m-1} \right ) \]

Further rewriting by grouping the terms with the same unknown,

\[ c^{n+1}_m = \left ( 1 -2q \right ) c^n_m + \left ( q - \frac 12 \sigma \right ) c^n_{m+1} + \left ( q + \frac 12 \sigma \right ) c^n_{m-1} \]

Now, assume that \(c^n_m \geq 0\), \(c^n_{m+1} \geq 0\) and \(c^n_{m-1} \geq 0\), then the coefficients \(1 -2q\), \(q - \frac 12 \sigma\) and \(q + \frac 12 \sigma\) must be non-negative in order to get \(c^{n+1}_m \geq 0\). Hence,

\[ 1-2q \geq 0 \quad \Rightarrow \quad q \leq \frac 12 \]

Note that

\[ \frac{\sigma}{q} = P_{\Delta} \]

so that

\[ q - \frac 12 \sigma \geq 0 \quad \Rightarrow \quad P_{\Delta} \leq 2 \]

and

\[ q + \frac 12 \sigma \geq 0 \quad \Rightarrow \quad -2 \leq P_{\Delta} \]

The first condition is recognized as the stability condition for the heat equation while the second one is the condition that we have found for the stationary advection-diffusion equation.

Instead of forward Euler we may choose the backward Euler scheme which is unconditionally stable but results into a system of equations. Also, regarding the advection term, we may choose a first order upwind scheme instead of central differences.

We conclude this section by noting that, in addition to the schemes discussed, many other numerical schemes exist for the advection-diffusion equation, each with specific properties regarding accuracy and stability. Such schemes are usually discussed in scientific journals.