# Matplotlib compatibility patch for Pyodide
import matplotlib
if not hasattr(matplotlib.RcParams, "_get"):
    matplotlib.RcParams._get = dict.get

2.3. Finite Difference Method

Consider the following equation that describes the growth of an ice layer assuming that the air and water temperatures are constant:

\[ \rho_{\mathrm{ice}}\frac{dh_{\mathrm{ice}}}{dt}=-k_{\mathrm{ice}}\frac{T_{\mathrm{water}}-T_{\mathrm{air}}}{h_{\mathrm{ice}}} \]

where \(h_{\mathrm{ice}}\) is the ice thickness, \(\rho_{\mathrm{ice}}\) ice density and \(k_{\mathrm{ice}}\) refers to the heat transfer capabilities of the ice.

Since it involves the derivative of \(h_{\mathrm{ice}}\), it is a differential equation. Let’s use it as an example to illustrate how we can solve differential equations approximately by using numerical techniques. The technique we will be using in this chapter is called the finite difference method (FDM). The basic idea behind this method is to approximate the derivatives in the differential equation using numerical differences, just like the forward, backward and central differences treated in the previous chapters. In essence, the finite difference method thereby transforms a differential equation into an algebraic form (discretization).

In our example, the growth rate (derivative) of the ice thickness, \(\frac{dh_{\mathrm{ice}}}{dt}\), can be approximated with one of the numerical derivatives. The resulting equation can be solved for the ice thickness in the next time step.

If we apply this procedure, we will not end up with a continuous solution, but with a solution at a discrete number of points. Therefore, we need to define the solution domain. For this example, an inital and an end time \([a,b]\) are needed, where \(a\) and \(b\) are called end points. The domain between these points is represented as grid points and therefore in a number of subintervals \(N\). The length of the subinterval is \(h=(b-a)/N\).

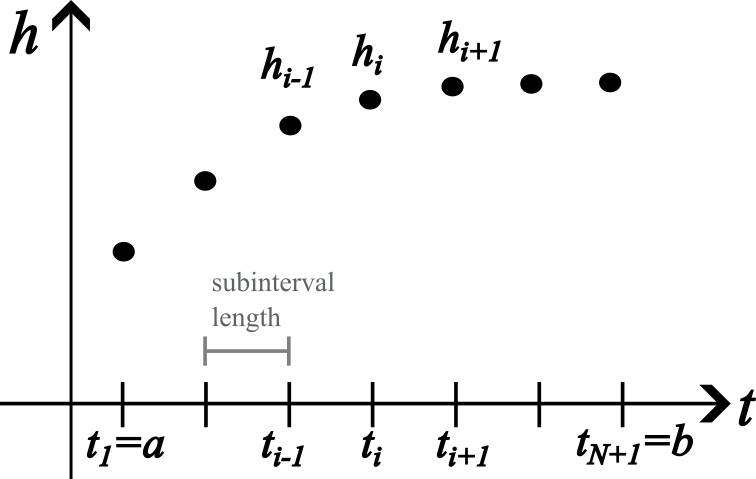
Fig. 2.4 Discretized differential equation ``

The figure above shows the grid of which the following property holds:

\[ a=t_1 < t_2 < ..<t_{N}< t_{N+1}= b \]

The points \(t_i\) on the grid are called nodes. Just note that your indexing is a choice. For example \(i\) can be for \(i = (1,2,...,N, N+1)\) as shown in the figure above. The indexing can also start at 0 where \(i = (0,1,...,N-1, N)\).

Lets simplify the above ice equation and put it in a standard ODE form:

\[ \frac{dh}{dt}= f \]

We can rewrite this equation in a discretized form:

\[ h'_i = f_i \]

Note that \(h'_i\) is the first derivative at node \(i\) and at that node is equal to function \(f_i\). Using FDM we numerically compute the solution \(h_i\) at each node \(t_i\) The connection between the derivative \(h'_i\) and \(t_i\) can be made by using Taylor series expansions.

Attribution

This chapter is written by Jaime Arriaga Garcia, Anna Störiko, Justin Pittman and Robert Lanzafame. Find out more here.