2.2. The First Derivative

Note

Important things to retain from this block:

• Understand what the derivative represents

• Recognize that the derivative can be approximated in different ways

In your calculus classes, you might remember working with the analytical definition of a derivative, such as \(\frac{df}{dx}\). This involved finding the limit as the distance between two points becomes infinitesimally small.

Definition:

The derivative of a function \(f(x)\) evaluated at the point \(x_0\) is

\[ \frac{df}{dx}\bigg\rvert_{x_0}=f'(x_0)=\lim_{x \to x_0}\frac{f(x)-f(x_0)}{x-x_0}. \]

Numerically:

\(x - x_0\) cannot tend to 0! Thus:

\[ f'(x_0) \approx \frac{f(x)-f(x_0)}{\Delta x}, \hspace{3mm} \text{where } \Delta x=x-x_0. \]

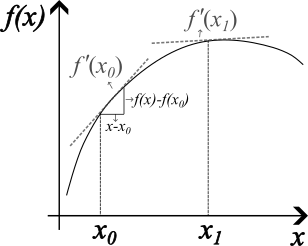
Fig. 2.2 derivatives of a function \(f(x)\) at a specific points \(x_0\) and \(x_1\)

What does the derivative represents? A rate of change! In this case, how fast \(f(x)\) changes with respect to \(x\) (or in the direction of \(x\)). The derivative can also be with respect to time or another independent variable (e.g., \(y,z,t,etc\)). Look at the figure above. The first derivative evaluated at \(x_0\) is illustrated as a simple slope, as is the first derivative evaluated at \(x_1\) . You can also see that the rate of change at \(x_0\) is larger than at \(x_1\).

Numerical Freedom to compute derivatives

In the Figure above, the derivative approximation was illustrated arbitrarily using two points: the one at which the derivate was evaluated and another point in front of it. However, there are more possibilities. Instead of using absolute points at \(x_{-1,0,1}\) a more general notation is used: \(x_{i-1,i,i+1}\). The simplest ways to approximate the derivative evaluated point \(x_i\) is to use two points:

\[ \text{forward: }\hspace{3mm} \frac{df}{dx}\bigg\rvert_{x_i}\approx\frac{f(x_{i+1})-f(x_{i})}{x_{i+1}-x_i} \hspace{5mm} \text{backward: } \hspace{3mm} \frac{df}{dx}\bigg\rvert_{x_i}\approx\frac{f(x_{i})-f(x_{i-1})}{x_{i}-x_{i-1}} \hspace{5mm} \text{central: } \hspace{3mm} \frac{df}{dx}\bigg\rvert_{x_i}\approx\frac{f(x_{i+1})-f(x_{i-1})}{x_{i+1}-x_{i-1}} \]

Note that the finite difference formula requires distances \(x_{i+1}-x_i\) and \(x_i-x_{i+1}\). In the next section (Finite Difference Method), we will have a closer look at defining these points. Afterwards, we will dive deeper into why the derivative approximations presented on this page are valid and how accurate they are, making use of Taylor series expansions.

Fig. 2.3 graphs illustrating three different ways to approximate derivatives.

Attribution

This chapter is written by Jaime Arriaga Garcia, Anna Störiko, Justin Pittman and Robert Lanzafame. Find out more here.