2.6. Initial Value Problem for ODE: single-step methods

Let’s look back at what we have achieved in the first part of this chapter:

• We can use finite differences to numerically approximate derivatives

• We can derive these finite difference approximations from a Taylor series expansion, giving us an idea about the error of the approximation.

Next, let us see how we can apply these concepts in order to numerically integrate (that is, solve) ODEs.

The solution process of an ODE is performed by steps. In a single-step approach, the solution of the following step depends only on the current one. In a multiple step method, the solution of the next step is calculated from several steps. A multiple step approach is more accurate, you can think of a similar construct as the higher-order derivatives treated previously.

Consider a first-oder ODE with the general form:

\[ \frac{dy}{dx} = f(x, y) \]

One initial condition is needed to find only one solution. Without it, there would be an infinite number of solutions possible. The initial condition is:

\[ y(x_0)=y_0 \]

Forward (Explicit) Euler

The simplest method for integrating initial value problems is the forward Euler scheme. It can be derived from the forward finite difference approximation of the derivative. Recall the forward finite difference formula:

\[ y'(x_i)=\frac{y(x_{i+1})-y(x_i)}{\Delta x} + \mathcal{O}(\Delta x) \]

where

\[ x_{i+1}=x_i+\Delta x \]

For simplicity, we can also define \(y_{i} = y(x_{i})\) and write:

\[ y'(x_i)=\frac{y_{i+1}-y_i}{\Delta x} + \mathcal{O}(\Delta x) \]

Now we can solve this expression for the state at the new time step, \(y_{i+1}\):

\[ y_{i+1} = y_i + \Delta x y'(x_i) + \mathcal{O}(\Delta x^2) \]

Ignoring the error terms, the forward Euler formula becomes:

\[ y_{i+1} = y_i + \Delta x f(x_i, y_i) \]

where we substituted \(y'(x_i) = f(x_i, y_i)\). Note that the derivative of \(y\) (the slope) is evaluated at the current time step \(x_i\). This makes the forward Euler scheme an explicit method. Although simple, it contains the basic characteristics as more advanced and accurate methods.

The solution starts at \(i=0\) given by the initial condition, then \(i\) is increased to 1 where the values are calculated using the previous equations. This loop continues until the points cover the desired domain.

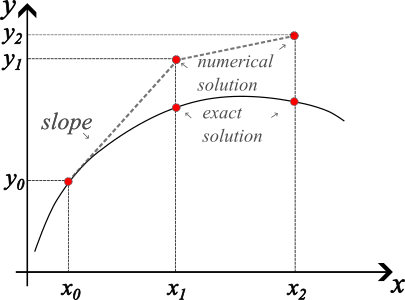
Fig. 2.11 Illustrating the forward Euler method

Example

Consider the following equation:

\[ \frac{dy}{dx}= y'=-\alpha y \]

We want to know the solution in the domain \([a=0,b=30]\). The initial condition is \(y(x_0)=1\) and the step size is \(\Delta x = 0.2\).

The discretization of the differential equation transforms the problem into an algebraic one. Following the formula of explicit Euler for the discretization yields:

\[ y_{i+1}= y_i + \Delta x \,y^\prime_i = y_i - \Delta x\, \alpha \,y_i \]

The following code snippet implements the forward Euler method for this example.

import numpy as np
import matplotlib.pyplot as plt

dx = 0.2
x = np.arange(0, 30 + dx, dx)
y = np.zeros(len(x))

##-----------------------------
##Forward Euler Implementation
##-----------------------------
alpha = 1
y[0] = 1
for i in range(len(x) - 1):
    y[i + 1] = y[i] + dx * (-alpha * y[i])
##------------------------------

y_exact = np.exp(-alpha * x)
plt.plot(x, y_exact)
plt.plot(x, y)
plt.legend(["exact solution", "Forward Euler solution"])

Exercise

Use the forward Euler to approximate the solution to the initial-value problem.

\[ \frac{dy}{dt}= y^2, \hspace{5mm}, 0\leq t \leq 1 \]

\[ y(t_0)= 1 \]

with \(\Delta t=0.5\)

Solution

\(t_0= 0, t_1= 0.5, t_2= 1\)

Use the forward Euler:

\[ y_{i+1}=y_i+\Delta x \cdot y'_{i} \]

for i =0

\[ y_{1}=y_0+\Delta x \cdot y'_{0} = 1+ 0.5 \cdot 1 = 1.5 \]

for i = 1

\[ y_{2}=y_1+\Delta x \cdot y'_{1} = 1.5+ 0.5 \cdot 1.5^2 = 2.625 \]

The approximated solution is 2.625

Error analysis

There are two types of errors: round-off and truncation errors. The round-off error is due to the computer’s limitation to represent a floating number (decimal). To illustrate it consider the following: the difference between 1 and 0.9 is 0.1. If you subtract 0.1 from itself, you should obtain 0, even if this subtraction is repeated ten thousand times. However, in practice, an extremely small error accumulates over each repetition, so the result will not be zero. The following code demonstrates this behavior, using floating-point numbers with varying precision.

def accumulated_error(a, b, solution, iterations):
    error = solution - np.abs(a - b)
    error_accumulated = 0
    for i in range(iterations):
        error_accumulated = error_accumulated + error

    return error_accumulated


print(
    "Error using 16 bits of memory = ",
    accumulated_error(np.float16(1.0), np.float16(0.9), np.float16(0.1), 10000),
)
print(
    "Error using 32 bits of memory = ",
    accumulated_error(np.float32(1.0), np.float32(0.9), np.float32(0.1), 10000),
)
print(
    "Error using 64 bits of memory = ",
    accumulated_error(np.float64(1.0), np.float64(0.9), np.float64(0.1), 10000),
)

As you can see, this simple operation can give discernible errors. Imagine a computation spanning 100 years with a time step of seconds and more complex operations: the round-off error will be present! As you can see, this can be reduced by increasing the precision or the number of digits used to represent numbers but be careful, this is not free as the memory the computer uses increases as well as the computation time.

The truncation error is related to the method chosen to approximate the slope. The error can be obtained using our reliable Taylor series expansion which gives the exact solution. Therefore the truncation error per step is:

\[ \text{Truncation error }= y^{TSE}(x_{i+1}) - y^{\text{Forward Euler}}(x_{i+1}) \]

\[ \text{Truncation error }= y(x_i)+\Delta x y'_i +\frac{(\Delta x)^2}{2!} y''_i + ... - y(x_i)-\Delta x y'_i \approx \mathcal{O}(\Delta x^2) \]

The total truncation error accounts for the number of steps as:

\[ \text{Total truncation error } \approx \sum_{i=0}^{n-1} \frac{(\Delta x)^2}{2!} y''_i \approx \frac{(\Delta x)^2}{2!} \frac{b-a}{\Delta x} \bar{y}'' \approx \mathcal{O}(\Delta x) \]

Because this total truncation error is of first order, the forward Euler method is referred to as a first-order method.

Stability

The error that is introduced in each step of the numerical solution ideally does not to increase as the solution advances. Under a well posed and proper solution, the error is expected to reduce with smaller steps. In some cases, the error increases without bound as the solution advances from the initial condition (even with smaller steps): the solution becomes unstable. The stability depends on the numerical method, the step size and the behavior of the differential equation. Therefore, the stability conditions will differ when applying the same numerical method to different equations.

Let’s consider the stability of the forward Euler method applied to a more general form of the problem above.

\[ \frac{dy}{dx} = y'=-\alpha y \]

With initial condition \(y(0)=1\) and \(\alpha>0\), the exact solution is:

\[ y^{\text{exact}}(x_{i})=y_0 e^{-\alpha x_{i}} \]

The forward Euler equivalent is

\[ y_{i+1}=y_{i}-\alpha y_i \Delta x=y_i(1-\alpha \Delta x) \]

Following the initial steps of the numerical solution a pattern arises:

\[ y_{1}=y_0(1-\alpha \Delta x) \]

\[ y_{2}=y_1(1-\alpha \Delta x) =y_0(1-\alpha \Delta x)^2 \]

\[ y_{3}=y_2(1-\alpha \Delta x) =y_0(1-\alpha \Delta x)^3 \]

\[ y_{n}=y_0(1-\alpha \Delta x)^n \]

Comparing this last equation with the exact solution, it can be seen that the term \((1-\alpha \Delta x)^n\) in the numerical solution is approximating the term \(e^{-\alpha \Delta x_i}\) in the exact solution. The latter tends to decay with larger values of \(x_i\) and positive \(\alpha\). To make sure that the term \((1-\alpha \Delta x)^n\) decays with larger \(n\) values \(1-\alpha \Delta x\) should be less than \(|1|\), i.e.,

\[ |1-\alpha \Delta x| < 1 \implies 0 < \alpha \Delta x < 2 \]

Click here for a more detailed derivation

\[ -1 <1-\alpha \Delta x < 1 \]

Subtract 1 of both sides

\[ -2 <-\alpha \Delta x < 0 \]

Divide by -1

\[ 0 <\alpha \Delta x < 2 \]

This is the stability criterion. If we do not comply with it, the solution will be unstable. We can say that the forward Euler scheme is conditionally stable. This is true for every explicit numerical method.

Exercise

Lets go back to the last example described in the code above (for \(\alpha=1\)).

\[ \frac{dy}{dx}= y'=-y \]

We want to know the solution in the domain \([a=0,b=30]\). The initial condition is \(y(x_0)=1\) and the step size is \(\Delta x = 0.2\).

What is the step size at which the problem described using the forward Euler method becomes unstable? Feel free to use the interactive figure below and change \(dx\) to test what happens when the step size becomes larger.

Click rocket –>Live Code to interact with the plot below

import numpy as np
import matplotlib.pyplot as plt
from ipywidgets import interact
import ipywidgets as widgets


def forward_euler(dx):
    # Define the x range and initialize y
    x = np.arange(0, 30 + dx, dx)
    y = np.zeros(len(x))

    # Forward Euler Implementation
    alpha = 1
    y[0] = 1
    for i in range(len(x) - 1):
        y[i + 1] = y[i] + dx * (-alpha * y[i])

    x_exact = np.arange(0, 30 + dx, 0.2)
    # Exact solution
    y_exact = np.exp(-alpha * x_exact)

    # Plot both solutions
    plt.figure(figsize=(8, 5))
    plt.plot(x_exact, y_exact, label="Exact solution", linestyle="--")
    plt.plot(x, y, label="Forward Euler solution", marker="o")
    plt.legend()
    plt.title(f"Forward Euler with dx = {dx}")
    plt.xlabel("x")
    plt.ylabel("y")
    plt.grid(True)
    plt.show()


# Create an interactive slider for dx
interact(
    forward_euler,
    dx=widgets.FloatSlider(value=0.2, min=0.01, max=3.0, step=0.01, description="dx"),
);

Solution

You can see in the interactive figure above that when the step size becomes larger the forward Euler solution becomes less accurate. You can also see that when the step size becomes bigger than 2 the forward Euler solution starts to blow up. This is because the stability criterion of the forward Euler method is violated.

\[ 0 <\alpha \Delta x < 2 \]

When \(\alpha=1\), then \(\Delta x < 2\) (Note that \(\Delta x\) cannot be negative and therefore will always be greater than 0.)

Backward (Implicit) Euler

Just as the forward Euler method is the simplest explicit method, the backward Euler method is the simplest implicit method. Both methods look very similar, but the key difference is the point where the slope, given by \(f(x, y)\), is evaluated. Remember that in the explicit Euler scheme, we evaluate the slope at the current value \(x_i\). In contrast, in the backward Euler scheme, the slope is computed at the next step, \(x_{i+1}\).

\[ x_{i+1}=x_i+\Delta x \]

\[ y_{i+1}=y_i+\Delta x \cdot \text{slope} \rvert_{i+1}=y_i+\Delta x \cdot f(x_{i+1}, y_{i+1}) \]

That is, the slope depends on the unknown value \(y_{i+1}\). This is why the backward Euler scheme is an implicit method.

Exercise

Derive the backward Euler formula from the backward finite difference approximation for the first derivative (presented in Section 2.4).

Solution

The backward finite difference approximation for the first derivative of a function \(y\) at point \(x_{i+1}\) is:

\[ y'(x_{i+1}) = \frac{y(x_{i+1}) - y(x_{i+1} - \Delta x)}{\Delta x} + \mathcal{O}(\Delta x) \]

Since \(x_{i+1} - \Delta x = x_i\), we can write:

\[ y'(x_{i+1}) = \frac{y(x_{i+1}) - y(x_i)}{\Delta x} + \mathcal{O}(\Delta x) \]

Multiplying by \(\Delta x\) yields:

\[ \Delta x \, y'(x_{i+1}) = y(x_{i+1}) - y(x_i) + \mathcal{O}(\Delta x^2) \]

Now, we solve for \(y(x_{i+1})\):

\[y(x_{i+1}) = y(x_i) + \Delta x \, y'(x_{i+1}) + \mathcal{O}(\Delta x^2)\]

Defining \(y_i = y(x_i)\) and \(y_{i+1} = y(x_{i+1})\), and considering that \(y'(x_{i+1}) = f(x_{i+1}, y_{i+1})\) we have:

\[y_{i+1} = y_i + \Delta x \, f(x_{i+1}, y_{i+1}) + \mathcal{O}(\Delta x^2)\]

Let’s consider the same problem as before:

\[ \frac{dy}{dx}= y'=-\alpha y \]

We want to know the solution in the domain \([a=0,b=30]\). The initial condition is \(y(x_0)=1\) and the step size is \(\Delta x = 0.2\).

The discretization of the differential equation transforms the problem into an algebraic one. Plugging the ODE into the formula for the implicit Euler scheme yields:

\[ y_{i+1}= y_i - \Delta x \cdot \alpha \cdot y_{i+1} \]

We bring all unknowns to the left side:

\[ y_{i+1}+ \Delta x \cdot \alpha \cdot y_{i+1} = y_i \]

Finally, we solve for \(y_{i+1}\):

\[ y_{i+1}= y_i/(1+\Delta x \cdot \alpha) \]

In the following code, Implicit Euler is implemented.

dx = 0.3
x = np.arange(0, 30 + dx, dx)
y = np.zeros(len(x))

##-----------------------------
##Backward Euler Implementation
##-----------------------------
alpha = 1
y[0] = 1
for i in range(len(x) - 1):
    y[i + 1] = y[i] / (1 + dx * alpha)
##------------------------------

y_exact = np.exp(-alpha * x)
plt.plot(x, y_exact)
plt.plot(x, y)
plt.legend(["exact solution", "Backward Euler solution"])

You can see that the result is similar to the forward Euler solution, except that the curve for the backward Euler scheme is slightly above the exact solution. This makes sense as the derivative is taken at the end of the integration interval. For exponential decay, the slope decreases throughout the integration interval but we assume that it is constant. If we evaluate it at the end of the integration interval (backward Euler), we underestimate the slope. In contrast, the explicit (forward Euler) solution overestimates the slope.

The round-off errors and truncation errors are similar for both methods. Backward Euler is also a first-order method. But what about the stability?

Stability

Exercise:

Modify the step size in the Implicit Euler code, try to make the solution unstable. What do you notice?

import numpy as np
import matplotlib.pyplot as plt
from ipywidgets import interact
import ipywidgets as widgets


def backward_euler(dx):
    # Define the x range and initialize y
    x = np.arange(0, 30 + dx, dx)
    y = np.zeros(len(x))

    ##-----------------------------
    ##Backward Euler Implementation
    ##-----------------------------
    alpha = 1
    y[0] = 1
    for i in range(len(x) - 1):
        y[i + 1] = y[i] / (1 + dx * alpha)
    ##------------------------------

    x_exact = np.arange(0, 30 + dx, 0.2)
    # Exact solution
    y_exact = np.exp(-alpha * x_exact)

    # Plot both solutions
    plt.figure(figsize=(8, 5))
    plt.plot(x_exact, y_exact, label="Exact solution", linestyle="--")
    plt.plot(x, y, label="Backward Euler solution", marker="o")
    plt.legend()
    plt.title(f"Backward Euler with dx = {dx}")
    plt.xlabel("x")
    plt.ylabel("y")
    plt.grid(True)
    plt.show()

# Create an interactive slider for dx
interact(
    backward_euler,
    dx=widgets.FloatSlider(value=0.2, min=0.01, max=5.0, step=0.01, description="dx"),
);

Let’s understand what happens by following the same procedure as for the stability analysis of explicit Euler.

The exact solution is the same:

\[ y^{\text{exact}}(x_{i})=y_0 e^{-\alpha x_{i}} \]

For the numerical solution, the numerical solution pattern is slightly different:

\[ y_{1}=y_0\left(\frac{1}{1+\alpha \Delta x}\right) \]

\[ y_{2}=y_1\left(\frac{1}{1+\alpha \Delta x}\right) =y_0\left(\frac{1}{1+\alpha \Delta x}\right)^2 \]

\[ y_{3}=y_2\left(\frac{1}{1+\alpha \Delta x}\right) =y_0\left(\frac{1}{1+\alpha \Delta x}\right)^3 \]

\[ y_{n}=y_0\left(\frac{1}{1+\alpha \Delta x}\right)^n \]

This last term to the power \(n\) approximates the decaying exponential in the exact solution, just like in the explicit Euler method. Here, the only condition that must be satisfied for stability is

\[\left|\frac{1}{1+\alpha \Delta x}\right| < 1\]

This can be expressed as:

\[ -1 <\frac{1}{1+\alpha \Delta x} < 1\]

Lets first look at the right side condition \(\frac{1}{1+\alpha \Delta x} < 1\).

If we multiply by the term \(1+\alpha \Delta x\), we get:

\[ 1 < 1+\alpha \Delta x \]

As \(\alpha\) is positive and the step size must be larger than 0, the right side of the criterion is always true.

Lets now look at the left side condition \(-1 <\frac{1}{1+\alpha \Delta x}\):

We again multiply by \(1+\alpha \Delta x\):

\[ -1 - \alpha \Delta x < 1 \]

Again this left side criterion always holds.

Hence, an implicit backward Euler scheme is unconditionally stable. This is also the case for more advanced implicit schemes.

Global errors

The global error is the sum of round-off and total truncation errors. The plot below displays the global errors for both the forward and backward Euler methods, alongside the reference line representing the slope of the truncation error \(\mathcal{O}(\Delta x)\) (1 to 1). As shown, the global errors for both methods align with the expected slope, indicating that the errors decrease in accordance with the methods’ first-order accuracy.

\[ \text{Global Error} = \sqrt{\frac{1}{n} \sum_{i=1}^{n} \left( y_i - y_{\text{exact},i} \right)^2} \]

import numpy as np
import matplotlib.pyplot as plt


def global_error(dx_values):
    errors_forward = []
    errors_backward = []

    for dx in dx_values:
        x = np.arange(0, 30 + dx, dx)
        y_forward = np.zeros(len(x))
        y_backward = np.zeros(len(x))

        alpha = 1
        y_forward[0] = 1
        for i in range(len(x) - 1):
            y_forward[i + 1] = y_forward[i] + dx * (-alpha * y_forward[i])

        y_backward[0] = 1
        for i in range(len(x) - 1):
            y_backward[i + 1] = y_backward[i] / (1 + dx * alpha)

        y_exact = np.exp(-alpha * x)
        n = (30 - 0) / dx
        # Compute the global error (L2 norm) for both methods
        error_forward = np.sqrt((1 / (n - 1)) * np.sum((y_forward - y_exact) ** 2))
        error_backward = np.sqrt((1 / (n - 1)) * np.sum((y_backward - y_exact) ** 2))

        errors_forward.append(error_forward)
        errors_backward.append(error_backward)

    # Plot the global error vs. dx in a loglog plot for both methods
    plt.figure(figsize=(8, 5))
    plt.loglog(
        dx_values, errors_forward, label="Forward Euler global error", marker="o"
    )
    plt.loglog(
        dx_values, errors_backward, label="Backward Euler global error", marker="s"
    )
    plt.loglog(
        dx_values,
        [dx**1 for dx in dx_values],
        label=r"$\mathcal{O} (\Delta x)$",
        linestyle="--",
    )

    plt.title(r"Global error comparison: Forward vs Backward Euler")
    plt.xlabel(r"$\Delta x$")
    plt.ylabel("Global error")
    plt.grid(True)
    plt.legend()
    plt.show()


dx_values = [0.00125, 0.0025, 0.005, 0.01, 0.02, 0.04, 0.08, 0.16, 0.32, 0.64]
# Call the function to plot the global error for both Forward and Backward Euler
global_error(dx_values)

Attribution

This chapter is written by Jaime Arriaga Garcia, Anna Störiko, Justin Pittman and Robert Lanzafame. Find out more here.