Filling a matrix

import numpy as np
import matplotlib.pyplot as plt

Now that we can visualize the contents of a matrix, let’s find an efficient way to fill it with specific values, focusing on creating specific patterns in an efficient way with our Python code. First, let’s recall a few more important things about Numpy arrays, focusing on the particular case of making 2-dimensional arrays to represent matrices.

One of the first things to remember is that Numpy uses a parameter shape to define the dimension and length of each axis of an array. For the 2D case, this means an \(m\)-by-\(n\) matrix is specified with a tuple containing two elements: (m, n).

Second, Numpy has many methods that make it easy to create a matrix and fill it with specific values. Check out a cool list here: Numpy array creation routines. Some commonly used methods are:

• np.zeros

• np.ones

• np.full

Third there are many Numpy methods that can modify an existing matrix (see the same list linked above), for example: np.fill_diagonal.

Finally, remember that arrays are quite smart when it comes to indexing. For example, we can use the range method (part of the standard Python library) to things to specific indices in an array.

With these tips in mind, let’s go over a few warm-up exercises to see how to easily manipulate matrices.

\(\text{Task 7.1:}\)

Refresh your memory on the range function by printing the documentation. Then comment the help line and confirm that you can use the function by using a list comprehension to print: a) values from 1 to 5, then b) values 2, 4, 6, 8, 10.

print('Part a:')
[print(i) for i in range(6)]

print('Part b:')
[print(i) for i in range(2, 11, 2)]

Part a:
0
1
2
3
4
5
Part b:
2
4
6
8
10

[None, None, None, None, None]

\(\text{Task 7.2:}\)

Use a Numpy method to create a 3x3 matrix filled with value 1.

A72 = np.ones((3,3))

\(\text{Task 7.3:}\)

Use a Numpy method to create a 3x3 matrix filled with value 3 on the diagonal and 0 elsewhere.

A73 = np.zeros((3,3))
np.fill_diagonal(A73, 3)

\(\text{Task 7.4:}\)

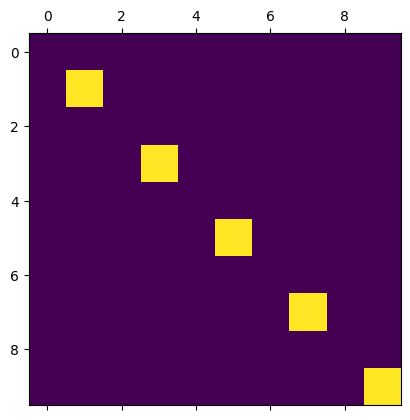
Use a Numpy method to create a 10x10 matrix, then assign every other element in the diagonal of the matrix to the value 1 using range and indexing. Use plt.matshow() to confirm that.

A74 = np.zeros((10,10))
A74[range(1, 10, 2), range(1, 10, 2)] = 1

plt.matshow(A74)
plt.show()

\(\text{Task 7.5:}\)

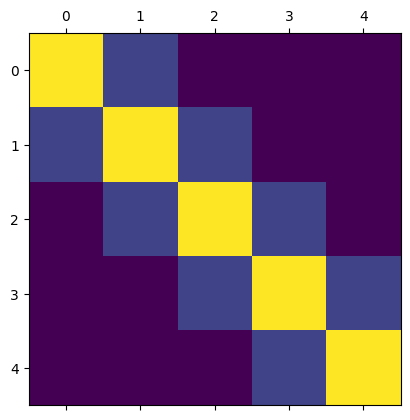
Use a Numpy method to create a 5x5 matrix, fill the diagonal with value 5, then use range and indexing to assign the diagonal above and below the center diagonal to the value 1. The solution is illustrated in the imported Markdown figure below.

A75 = np.zeros((5, 5))
np.fill_diagonal(A75, 5)
A75[range(4), range(1, 5)] = 1
A75[range(1, 5), range(4)] = 1

plt.matshow(A75)
plt.show()

\(\text{Task 7.6:}\)

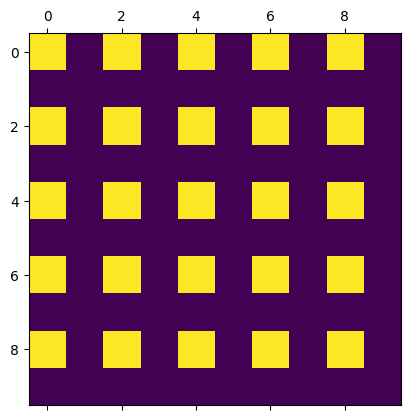
Create the matrix illustrated in the figure below, where the values are either 0 or 1.

A76 = np.zeros((10, 10))
for i in range(0, 10, 2):
    A76[i, range(0, 10, 2)] = 1

plt.matshow(A76)
plt.show()

\(\text{Task 7.7:}\)

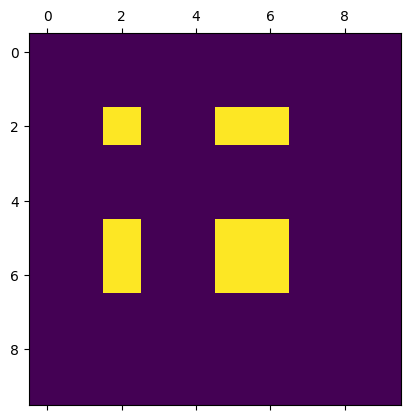
Until now, we have seen that we can use range indexing for indexing positions. However, we have the limit that the indexing always refers to ‘intersection’ of rows and columns: for the last exercise we had to repeat the indexing for multiple rows to get the ‘union’ of all indices with that row and column index. An alternative is using np.ix_() for indexing. This allows you to define the ‘union’ of multiple row and column indices more easily, as shown below with an example. Use this approach to create a checkboard pattern with blocks of 2x2 instead of 1x1 as in task 7.6.

A = np.zeros((10,10))
A[np.ix_([2,5,6],[2,5,6])] = 1

plt.matshow(A)
plt.show()

A77 = np.zeros((10,10))
A77[np.ix_([0,1,4,5,8,9],[0,1,4,5,8,9])] = 1

plt.matshow(A77)
plt.show()

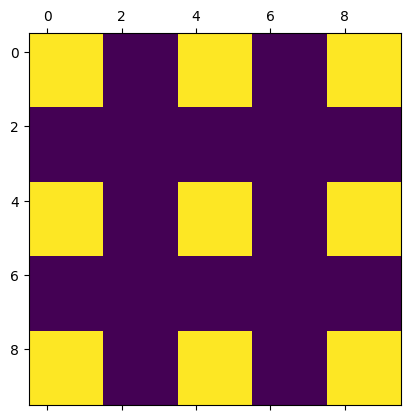
\(\text{Task 7.8:}\)

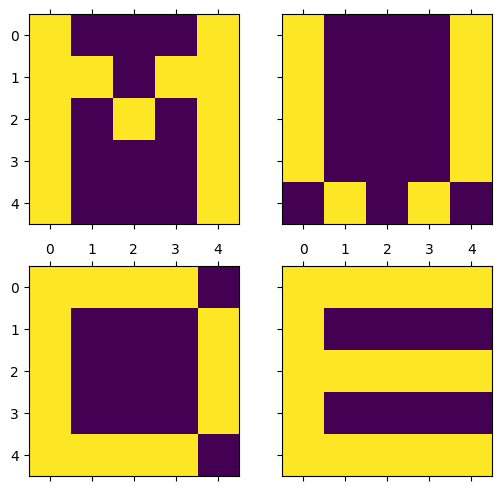
Try to create the following (sub-)matrices in the most efficient way using some of the above methods and plot them in a 2x2 setting using plt.subplots and matshow:

A1 = np.zeros((5,5))
A1[:,range(0,5,4)] = 1
A1[1,1] = 1
A1[2,2] = 1
A1[1,3] = 1

A2 = np.zeros((5,5))
A2[:, range(0,5,4)] = 1
A2[-1,:] = [0,1,0,1,0]

A3 = np.ones((5,5))
A3[np.ix_([1,2,3],[1,2,3])] = 0
A3[range(0,5,4),-1] = 0

A4 = np.ones((5,5))
A4[np.ix_([1,3],[1,2,3,4])] = 0


fig, ax = plt.subplots(2, 2, figsize=(6, 6), sharex=True, sharey=True)
ax[0, 0].matshow(A1)
ax[0, 1].matshow(A2)
ax[1, 0].matshow(A3)
ax[1, 1].matshow(A4)
plt.plot()

[]

By Tom van Woudenberg, Ronald Brinkgreve and Robert Lanzafame, Delft University of Technology. CC BY 4.0, more info on the Credits page of Workbook.