3.2. Complex Fourier Series

A quick recap

From the previous chapter, we have found that any periodic signal can be written into series of harmonically related sinusoids:

\[x(t)=a_0+\sum_{k=1}^{\infty}a_k\cos(k\omega_0 t)+\sum_{k=1}^{\infty}b_k\sin(k\omega_0 t), \hspace{10px}\text{with }\omega_0=\frac{2\pi}{T_0}\]

where the coefficients can be found as:

\[\begin{split}\begin{gather*}a_0=\frac{1}{T_0}\int_{T_0}x(t)dt\\ a_k = \frac{2}{T_0}\int_{T_0}x(t)\cos(k\omega_0 t)dt, \hspace{10px}\text{with } k\in\mathbb{N}^+\\ b_k = \frac{2}{T_0}\int_{T_0}x(t)\sin(k\omega_0 t)dt, \hspace{10px}\text{with } k\in\mathbb{N}^+\end{gather*}\end{split}\]

Now the same signal decomposition, but in a different form using complex algebra as commonly done in spectral analysis of signals, will be used.

Complex Algebra

\(j\): imaginary unit (or number) such that \(j^2=-1\)

\(e\): Euler’s number (base of the natural logarithm), \(e\approx 2.71\)

Euler’s formula:

\[\begin{split}\begin{gather*}e^{j\theta}=\cos\theta+j\sin\theta\\ e^{-j\theta}=\cos\theta-j\sin\theta\end{gather*}\end{split}\]

and, therewith:

\[\begin{split}\begin{gather*}e^{j\theta}+e^{-j\theta}=2\cos\theta\implies\cos\theta=\frac{1}{2}(e^{j\theta}+e^{-j\theta})\\ e^{j\theta}-e^{-j\theta}=2j\sin\theta\implies\sin\theta=\frac{1}{2j}(e^{j\theta}-e^{-j\theta})\end{gather*}\end{split}\]

Complex Fourier Series

\[x(t)=\sum_{k=-\infty}^{\infty}X_ke^{jk\omega_0 t}\]

First equation is known as synthesis equation of Fourier Series, as in contructs the signal using complex exponential basis functions

\[X_k=\frac{1}{T_0}\int_{T_0}x(t)e^{-jk\omega_0 t}dt, \hspace{10px}k\in\mathbb{Z}\]

Second equation is known as analysis equation of Fourier Series, as it allows us to analyze how signal can be represented by complex exponential basis functions (where index \(k\) refers to frequency \(k\omega_0=k2\pi f_0\)).

Derivation

MUDE Exam Information

This derivation is provided for additional insight and will not be part of the exam.

Start by substituting the complex exponential forms of both \(\cos(k\omega_0 t)\) and \(\sin(k\omega_0 t)\) into trigonometric series:

\[\begin{split}\begin{align}x(t)&=a_0+\sum_{k=1}^{\infty}a_k\textcolor{red}{\frac{1}{2}(e^{jk\omega_0 t}+e^{-jk\omega_0 t})}+\sum_{k=1}^{\infty}b_k\textcolor{green}{\frac{1}{2j}(e^{jk\omega_0 t}-e^{-jk\omega_0 t})}=\\&=a_0+\sum_{k=1}^{\infty}\underbrace{\frac{1}{2}(a_k-jb_k)}_{X_k}e^{jk\omega_0 t}+\sum_{k=1}^{\infty}\underbrace{\frac{1}{2}(a_k+jb_k)}_{X_{-k}}e^{-jk\omega_0 t}=\\&=a_0+\sum_{k=1}^{\infty}X_ke^{jk\omega_0 t}+\sum_{k=1}^{\infty}X_{-k}e^{-jk\omega_0 t}\end{align}\end{split}\]

If we replace the last term index \(-k\) for \(k\) then we get:

\[x(t)=a_0+\sum_{k=1}^{\infty}X_ke^{jk\omega_0 t}+\sum_{k=-1}^{-\infty}X_ke^{jk\omega_0 t}\]

As when \(k=0\) we have \(X_k=X_0=a_0\) and \(e^{jk\omega_0 t}=e^{j0\omega_0 t}=1\), then we can compact everything and write

\[x(t)=\sum_{k=-\infty}^{\infty}X_ke^{jk\omega_0 t}\]

where

\[X_k=\frac{1}{T_0}\int_{T_0}x(t)e^{-jk\omega_0 t}dt, \hspace{10px}k\in\mathbb{Z}\]

Coefficients

Real and complex Fourier series coefficients are related by:

\[\begin{split}X_k=\begin{cases}\frac{1}{2}(a_k-jb_k),\hspace{5px}k>0\\ \frac{1}{2}(a_{-k}+jb_{-k}),\hspace{5px}k<0\end{cases}\end{split}\]

so

\[\begin{split}\begin{gather*}X_1=\frac{1}{2}(a_1-jb_1), X_2=\frac{1}{2}(a_2-jb_2)\\ X_{-1}=\frac{1}{2}(a_1+jb_1), X_{-2}=\frac{1}{2}(a_2+jb_2)\end{gather*}\end{split}\]

And we clearly see that \(X_k=X^*_{-k}\), with \(*\) denoting the complex conjugate. The visual representation of \(X_k\) and \(X_{-k}\) will be, therefore:

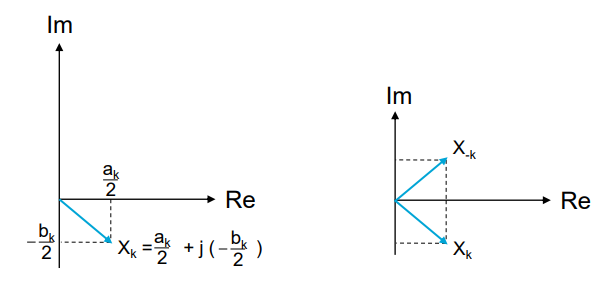
We have \(a_k=2\text{Re}(X_k)\) and \(b_k=-2\text{Im}(X_k)\) for \(k>0\)

Visualising complex coefficients \(X_k\) as vectors in complex plane: magnitude, or modulus (amplitude), and argument, or phase. We can write the coefficients in polar (or phasor) form:

\[X_k = |X_k|e^{j\theta_k}, \hspace{10px}\text{with } \theta_k=\angle X_k=\text{arg}(X_k) \hspace{10px}\text{for }-\infty<k<\infty (k\in\mathbb{Z})\]

and we find:

• Magnitude \(|X_k|=\frac{1}{2}\sqrt{a_k^2+b_k^2}\), k>0

• Argument \(\theta_k=\arctan\left(-\frac{b_k}{a_k}\right)\), k>0

For real signals \(x(t)\), as we use in this practical course, we have \(|X_k|=|X_{-k}|\) and \(\theta_k=-\theta_{-k}\)

Line Spectra

The complex exponential Fourier series coefficients

\[X_k=\frac{1}{T_0}\int_{T_0}x(t)e^{-jk\omega_0 t}dt, \hspace{10px}k\in\mathbb{Z}\]

• shows amplitudes of all phasors involved, through modulus of complex exponential coefficients \(|X_k|\) versus frequency \(kf_0\), yields amplitude spectrum (actually magnitude spectrum)

• shows phases of all phasors, through argument of the complex exponential coefficients \(\theta_k\) versus frequency \(kf_0\), yields phase spectrum

Example

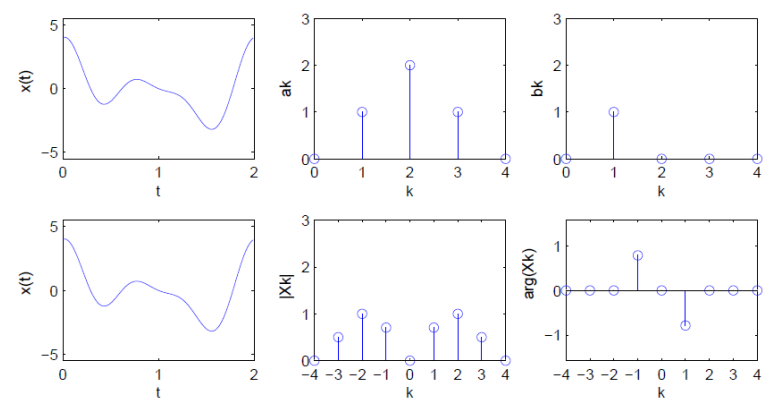
Consider the following signal, with period \(T_0=2s\), so \(f_0=0.5\) Hz, composed of three cosines and one sine:

\[x(t)=\cos(2\pi f_0t)+2\cos(2\pi 2f_0t)+\cos(2\pi 3f_0t)+\sin(2\pi f_0t)\]

Real and complex Fourier coefficients are shown below

Summary

The complex exponential Fourier series is given by

\[x(t)=\sum_{k=-\infty}^{\infty}X_ke^{jk\omega_0 t}\]

with coefficients

\[X_k=\frac{1}{T_0}\int_{T_0}x(t)e^{-jk\omega_0 t}dt, \hspace{10px}k\in\mathbb{Z}\]

The complex coefficients can be written in polar form: \(X_k=|X_k|e^{j\theta_k}\)

\[\text{with } \theta_k=\angle X_k=\text{arg}(X_k) \hspace{10px}\text{for }-\infty<k<\infty (k\in\mathbb{Z})\]

then, for real signals:

• magnitude: \(|X_k|=|X_{-k}|\), even function of \(k\) (and hence frequency \(kf_0\)) forming amplitude spectrum

• argument (or phase): \(\theta_k=-\theta_{-k}\), odd function of \(k\), forming phase spectrum

\(\implies\) periodic signal written in terms of sum of cosines and sines, together (pairwise) represented in complex exponentials

Attribution

This chapter is written by Christiaan Tiberius. Find out more here.