Exercise 1: Simple Exercise

MUDE Exam Information

For the exam, you are expected to have a clear understanding behind the Simplex method and how to do it. you will not need to do the calculations by hand in the exam or on Friday’s assignment.

Consider the following problem:

\[\max \left( Z \right) = 2{x_1} + 2{x_2}\]

such that

\[\begin{split}\begin{cases}2{x_1} + {x_2} \le 4 \\{x_1} + 2{x_2} \le 4 \\{x_1} + {x_2} \le 5 \\{x_1},{x_2} \ge 0 \end{cases}\end{split}\]

Task 1

Transform the problem into the augmented form

Solution

\[Z - 2{x_1} - 2{x_2} - 0{s_1} - 0{s_2} - 0{s_3} = 0\]

such that

\[\begin{split}\begin{cases}2{x_1} + {x_2} + s_1 = 4\\{x_1} + 2{x_2} + s_2 = 4 \\{x_1} + {x_2} + s_3 = 5 \\{x_1},{x_2},s_1,s_2,s_3 \ge 0 \end{cases}\end{split}\]

Task 2

Task 3

Why is your final table the optimal solution?

Solution

This is the optimal solution because all the coefficients are positive in the row of the objective function and this is a maximization problem.

Task 4

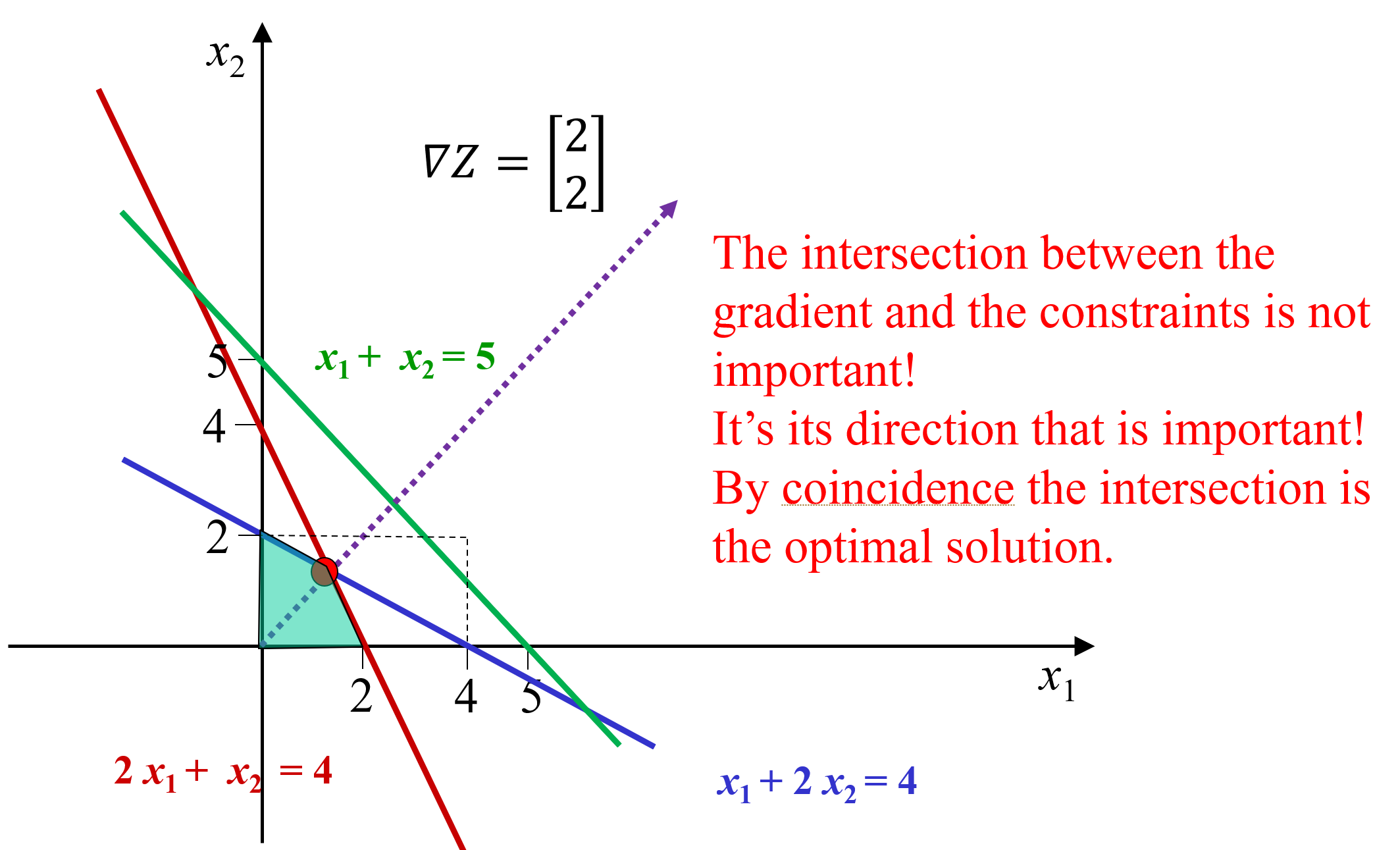
Find the graphical solution of this problem. Does it give the same solution as using the Simplex method?

Solution

Note: in this problem and solution the intersection between the gradient and the constraints is not important (see figure), but rather the direction that is important! It is a coincidence that the intersection is the optimal solution.

Attribution

This chapter is written by Gonçalo Homem de Almeida Correia, Maria Nogal Macho, Jie Gao and Bahman Ahmadi. Find out more here.