Uniform distribution

The uniform distribution is the simplest type of continuous parametric distribution and, as it is implied in its name, the PDF has a constant value along a given interval \([a,b]\), where \(a < b\). The PDF of the uniform is given by

\[ f(x) = \frac{1}{b-a} \hspace{1cm} \text{for} \ a\leq x \leq b \]

\[ f(x) = 0 \hspace{1cm} \text{otherwise} \]

Note that all values in the distribution are between the lower limit \(a\) and the higher limit \(b\) and are equally likely to occur. The left pannel of the figure below, shows an example of a uniform PDF with \(a=-1\) and \(b=1\).

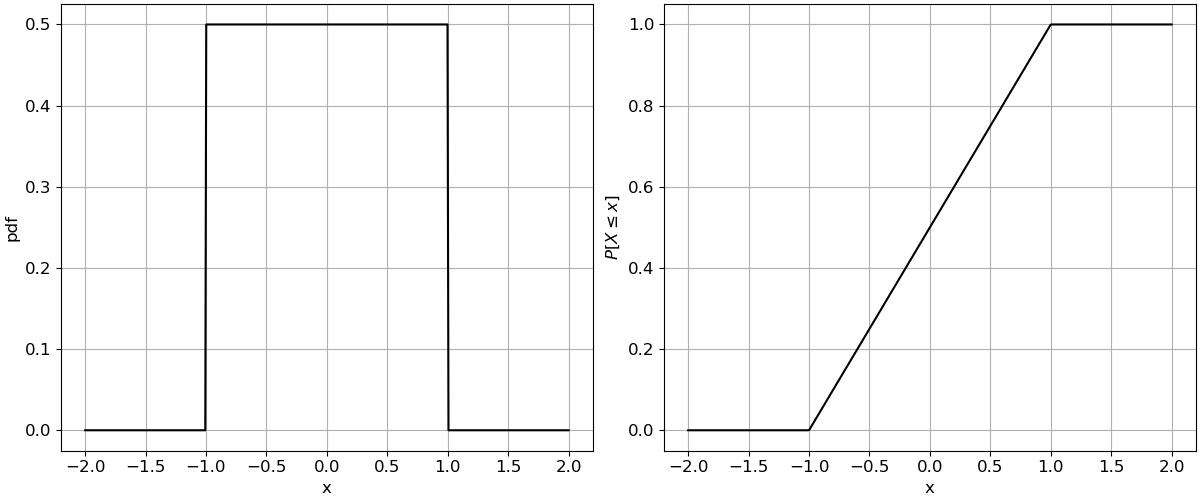
Fig. 5.11 Uniform distribution function: (left) PDF, and (right) CDF.

As seen in previous chapters, the CDF is the integral of the PDF. Thus, as we integrate over a constant, the CDF presents a linear shape, as shown in the right pannel of the figure above. Thus, the CDF is given as

\[ F(x) = 0 \hspace{1cm} \text{for} \ x<a \]

\[ F(x) = \frac{x-a}{b-a} \hspace{1cm} \text{for} \ a\leq x \leq b \]

\[ F(x) = 1 \hspace{1cm} \text{for} \ x>b \]

If we make \(a=0\) and \(b=1\), we obtain the standard or unity uniform distribution, which is used to generate random values from other distribution functions for simulation purposes.

Some properties

The mean of the uniform distribution can be computed based on its simple geometry as

\[ E[X]=\frac{1}{2}(a+b) \]

The variance is given by

\[ Var[X] = \frac{1}{12}(b-a)^2 \]

Finally, note that uniform distribution is symmetric and presents 0 skewness. Thus, the median and the mean are identical. This is, it does not present any tail.

Attribution

This chapter was written by Patricia Mares Nasarre and Robert Lanzafame. Find out more here.