import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

Notebook Gauss-Newton iteration for a point on a circle

If you want to download the notebook, select the .zip after clicking on .

Click –> Live Code on the top right corner of this screen and then wait until all cells are executed.

In this exercise we will consider the following problem:

we have a point on a circle with known radius \(r=2\) meters. We are interested in the unknown angle \(x=\alpha\). We do have an observation of both the \(u\)- and \(v\)-coordinate. Our observations are \(u=1.4957\) and \(v=1.5048\) m.

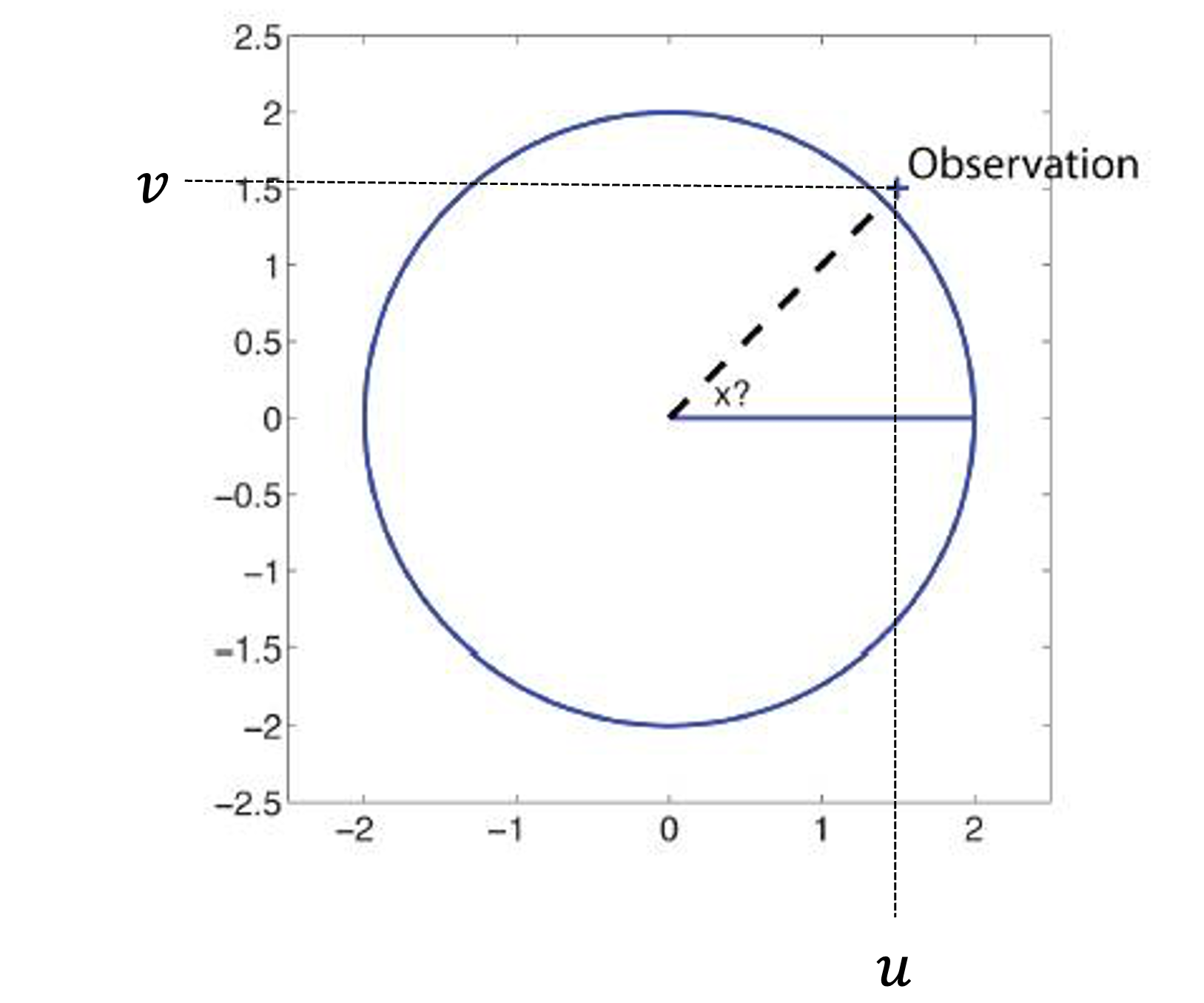
By completing the code below you will perform the Gauss-Newton iteration to obtain an estimate for the angle. Note that we express the angle in radians.

Our functional model is given by:

\[\begin{split} \mathbb{E}(Y)=\begin{bmatrix}2\cos x\\ 2 \sin x\end{bmatrix} \end{split}\]

We assume that both observables have a precision of 5 mm.

The observation vector y and inv_Sigma_Y\(=\Sigma_Y^{-1}\) are already defined.

You are asked to derive what the Jacobian matrix is and complete the code to compute:

y_comp \(=q(x_{[i]})\)

dy \(=\Delta y_{[i]}\)

J\(=J_{[i]}\)

Change the value of the initial value x_init to see the effect in the figures.

In this case we will not use a stop criterion for the iteration, but simply stop after N=10 iterations.

y = np.array([1.4957, 1.5048]) 
var_Y = 5e-3**2
inv_Sigma_Y = 1/var_Y * np.eye(2)

x_init = 2

N = 10
dx_i = np.zeros(N) # initialize the dx_i vector
x_i = np.zeros(N+1) # initialize the x_i vector
x_i[0] = x_init 

for i in np.arange(N):
    y_comp = np.array([ ? , ? ]) 
    dy = ?
    J = np.array([ ? , ? ]) 
    
    # note that (J.T @ inv_Sigma_Y @ J) is a scalar, therefore we 
    # use 1/(...) instead of np.linalg.inv(...)
    dx_i[i] = 1/(J.T @ inv_Sigma_Y @ J) * J.T @ inv_Sigma_Y @ dy 
    x_i[i+1] = x_i[i] + dx_i[i] 

# set final estimate equal to the last value in x_i and evaluate its precision
xhat = x_i[-1]
sigma_xhat = np.sqrt(1/(J.T @ inv_Sigma_Y @ J))

print(f'The final estimate for the angle is: {xhat:.3f} radians\n')
print(f'The precision of the estimated angle is: {sigma_xhat:.2e} radians')

fig, ax = plt.subplots(1, 2, figsize = (16, 6))
ax[0].plot(dx_i, 'r-o')
ax[0].set_xlabel('iteration number $i$', fontsize = 15)
ax[0].set_ylabel('$\Delta \hat{x}_{[i]}$ [rad]', fontsize = 15)
ax[0].grid()
ax[1].plot(x_i, 'r-o')
ax[1].set_xlabel('iteration number $i$', fontsize = 15)
ax[1].set_ylabel('$x_{[i]}$ [rad]', fontsize = 15)
ax[1].grid()

The left-side figure shows for each iteration the value of \(\Delta \hat{x}_{[i]}\), which should become smaller and smaller if all goes well. On the right-hand side you see how \(x_{[i]}\) is updated in each iteration step, where the final value will be used as our estimate \(\hat{x}=x_{[10]}\).

Solutions

y_comp = np.array([ 2 * np.cos(x_i[i]) , 2 * np.sin(x_i[i]) ])

dy = y - y_comp

J = np.array([ -2 * np.sin(x_i[i]) , 2 * np.cos(x_i[i]) ])

Attribution

This chapter was written by Sandra Verhagen. Find out more here.