Threshold & Declustering

In the previous chapter, we saw the Peak Over Threshold (POT) technique to sample extremes and we applied it to our time series. We used a threshold \(th = 2.5m\) and a declustering time \(dl = 48h\), obtaining the figure below. However, no justification was given for those parameters. In this section, we will start giving insight on how to select \(th\) and \(dl\), which is inherently a verification and validation process for our chosen distribution.

Fig. 7.16 Application of POT to \(H_s\) time series with \(th = 2.5m\) and \(dl = 48h\).

We also discussed previously that extreme observations tend to cluster in time and, thus, we need to ensure that only one extreme observation is sampled within each cluster to guarantee our assumption of iid observations. Thus, threshold and declustering time should be selected accounting for it. In addition, the concept of Poisson process and its relationship with EVA was introduced. It was concluded that by ensuring that the number of excesses per year followed a Poisson distribution, the sampled extremes were iid.

There are several techniques in the literature to support the decision-making process of selecting \(th\) and \(dl\) for POT. Here, we will start with the basic one (application of properties of Poisson distribution and hypothesis testing to check whether the number of excesses per year follows a Poisson distribution) which is the underlying assumption below the more complex techniques that we will see in subsequent sections.

We already applied POT with \(th = 2.5m\) and \(dl=48h\) to our example dataset. Let’s check whether those parameters are appropriate or we should change them. To do so, we are going to check if the number of excesses per year follows a Poisson distribution.

First step is to calculate the number of excesses we have per year and, with it, the empirical pmf and the empirical cdf. Remember that the pmf gives us \(P[X=x]\) and the cdf, \(P[X \leq x]\).

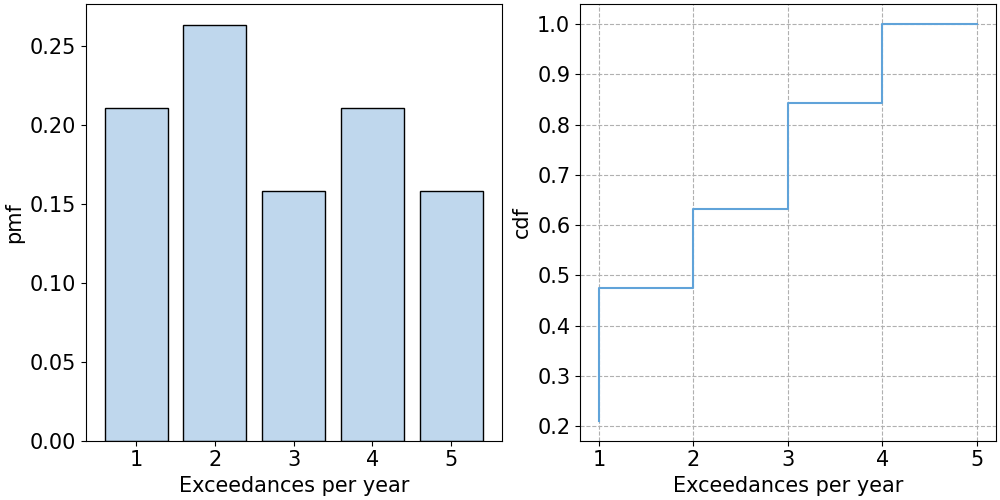
Fig. 7.17 Empirical pmf and cdf for number of excesses per year.

Now, we can fit a Poisson distribution to that empirical distribution and check whether the Poisson distribution is a reasonable model for our number of excesses per year.

We can fit such distribution using Moments method, which consists of estimating the parameters of the distribution based on the moments calculated from the data (mean, standard deviation…). Applying the properties of the Poisson distribution, \(E[X]=Var[X]=\lambda\), being \(\lambda\) the distribution parameter. Based on that, we can conclude:

• Using my observations, \(E[X]=2.84\) and \(Var[X]= 1.92\). Thus, \(E[X]=Var[X]\) is not true for our observations, but we can assume \(E[X]\approx Var[X]\).

• We can assume a fitted Poisson with \(\lambda = E[X]= 2.84\) for the subsequent analysis.

Once we have fitted the Poisson distribution, we can visually check the fit, as shown below. The figure on the left shows the supperposition of the empirical and fitted cdf. The figure on the right shows the empirical and estimated probabilities for number of excesses = 1, 2, … 5, namely the PP-plot. The fitting seems reasonable.

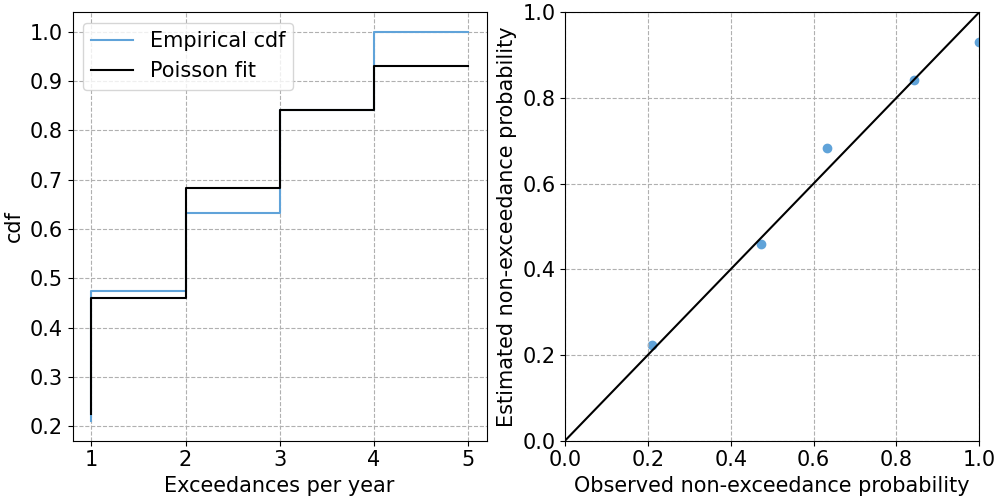
Fig. 7.18 Empirical pmf and cdf for number of excesses per year.

In order to further support our decision, we can perform a goodness-of-fit hypothesis test for discrete distributions, such as \(\chi^2\) test.

Let’s practice!

A scientist is analyzing the extreme precipitation rate events in a city and decided to apply POT to sample the extreme events. The scientist has chosen a threshold \(th=100 \ mm/h\) and declustering time \(dl= 2\) min. The following figure shows part of the timeseries together with the sampled extremes and the threshold.

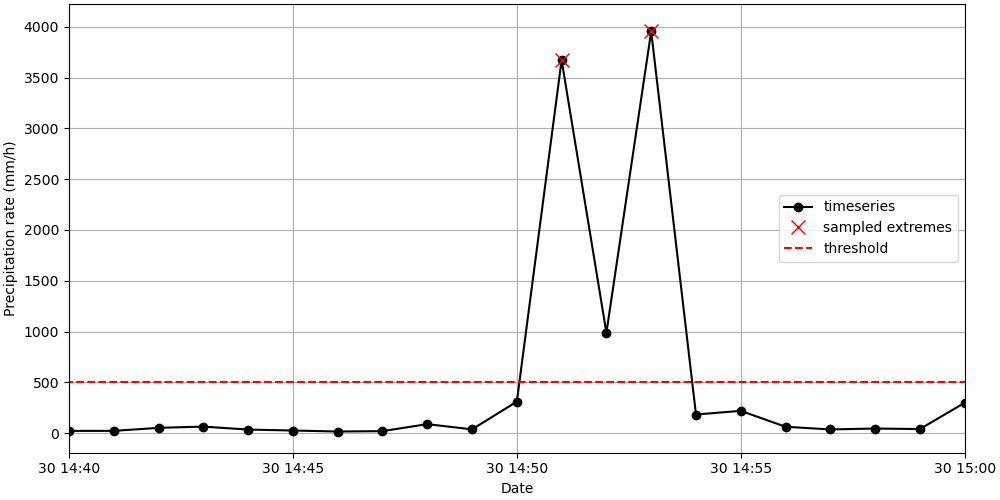
Fig. 7.19 Sampled extremes in the precipitation rate timeseries.

Do you think that the selected POT parameters (\(th\) and \(dl\)) are adequate?

Answer

The declustering time is not long enough to prevent POT to sample extremes belonging to the same storm, according to the above picture. Two extremes from the same storm event are sampled and, since they are generated by the same drivers, cannot be considered independent. Moreover, if we apply the knowledge on the physical phenomenon that the scientist is studying (a storm), we know that extreme storms are longer than a few minutes.

The scientist performs again the analysis with a different set of parameters and obtains a mean value of events per month of \(E[X]=3.33\) and a variance of \(Var[X]= 3.24\). Without further information, do you think that the select POT parameters are adequate?

Answer

Applying the properties of the Poisson distribution, \(E[X]=Var[X]=\lambda\), being \(\lambda\) the distribution parameter. Here \(E[X] = 3.33 \approx Var[X] = 3.24\). Therefore, the number of sampled events per time block (here, one month) seems to come from a Poisson distribution. This indicates that the sampled events are independent and, thus, the parameters of the POT analysis are adequate.